pdf / bibref / poster / code
- 1 Institut de Robòtica i Informàtica Industrial, Barcelona, Spain
- 2 Center for Visual Computing, Ecole Centrale de Paris, France
- 3 Galen, INRIA Saclay, France
This paper exploits segmentation to build appearance descriptors that can robustly deal with occlusion and background changes. We achieve this by leveraging soft segmentation data into the construction of the descriptor, downplaying measurements coming from areas that are unlikely to belong to the same region as the center of the descriptor. This technique is applicable to any image point (i.e. dense), has a small computational overhead, is very simple by design (one parameter), and can be applied to any SIFT-like descriptor defined over a spatial grid. We apply it to SIFT, and also to the Dense Scale and Rotation Invariant Descriptors (SID) [4], delivering descriptors that are densely computable, invariant to scaling and rotation, and robust to background changes. We use two different off-the-shelf, state-of-the-art techniques to compute soft segmentations (no need to reinvent the wheel!), and we apply it successfully to two different problems.
The problem: Invariant descriptors are still a major area of research in computer vision. This is particularly important for dense descriptors, as we cannot estimate local scale and orientation on arbitrary image locations. Recent works have addressed some of these issues, including scale- and/or rotation-invariance or non-rigid deformation. This works deals with occlusion effects. We are inspired by the Daisy paper [6], which reported substantial performance improvements in multi-view stereo by treating occlusion as a latent variable. Our main contribution in this work is a new approach to suppress background information during descriptor construction. For this we use soft segmentation masks to estimate the affinity of a point with its neighbors, and shun the information coming from regions which are likely to belong to other objects. We then apply these masks over the features. The next figure displays this process.

Left to right: Input image; RGB representation of the first three levels of the soft segmentation pixel embeddings; affinity between the pixel of interest and its neighbourhood; and the segmentation mask corresponding to a SIFT descriptor.
Soft segmentation masks
This problem is obviously connected with segmentation, which despite considerable progress remains an unsolved problem. We turn to algorithms which do not commit to a single 'hard' segmentation, but work with pixel affinities instead: these are what we call 'soft' segmentations. So as not to reinvent the wheel, we try two different off-the-shelf solutions: the approach of Maire et al [2] and the soft segmentations of Leordeanu et al [3]. The work of [2] combines multiple cues to estimate a boundary-based affinity, which is then ‘globalized’ by finding the eigenvectors of the relaxed Normalized cut criterion. The traditional approach would be to form a hard segmentation from the affinities, whereas we take them as pixel embeddings. As for [2], local color models are constructed around each pixel to build a large set of figure/ground segmentations, which are projected onto a lower-dimensional subspace through PCA, at a drastically smaller computational cost. Either approach gives us low-dimensional (8-10) embeddings, which bring together pixels which are likely to belong to the same region, and pull apart those that do not belong together. The affinity of two pixels is computed as the euclidean distance of their respective embeddings. For simplicity, we call the embeddings of [2] 'Eigen' of those of [3] 'SoftMask'. Note that we use either one embedding or the other, and do not try to combine them. The following figure shows some examples.

RGB representation of the first three levels of the pixel embeddings.
To take advantage of this we design masks similar in spirit to those of [6] during descriptor construction. This is applicable to any descriptor defined over regions around a feature point, such as SIFT's 4x4 grid. So for a descriptor computed on pixel \(\mathbf{x}\) over a grid \( \mathbf{G}^{[i]}(\mathbf{x}), i=1 \dots N \), we can define weights over each grid point as:
$$\mathbf{w}^{[i]} = \exp\left( -\lambda \cdot d(\mathbf{x},\mathbf{G}^{[i]}(\mathbf{x}))\right)$$ $$d(\mathbf{x},\mathbf{G}^{[i]}(\mathbf{x})) = \|y(\mathbf{x}) - y(\mathbf{G}^{[i]}(\mathbf{x})\|_2^2$$where \( y(\cdot) \) are the pixel embeddings of point \( \cdot \), and \( \lambda \) is our design parameter. To apply these masks we simply multiply the weights with the features \( \mathbf{D}(\mathbf{x}) \), where e.g. for SIFT \( \mathbf{D}^{[i]}(\mathbf{x}) \) are the entries of the cell positioned at \( [i], i=1,\dots,16 \) with the grid centered on \( \mathbf{x} \). This technique is directly applicable to any descriptor defined over a spatial grid, such as SIFT or Daisy itself. We also apply it to SID [4], which is described in the next section.
The Scale- and rotation-Invariant Descriptor (SID)
SID is a SIFT-like descriptor which is defined over a log-polar grid. If we sample the signal densely enough, scalings and rotations are equivalent to shifts on the matrix of measurements, plus the introduction and removal of some entries on the finer/coarser scales (see figure).
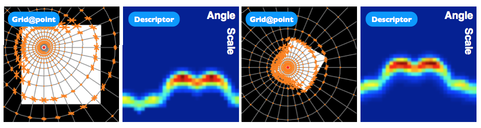
Feature representation for SID (over the spatial grid, before computing the Fourier Transform). See how changes in scale and rotation become shifts over the matrix.
Then, from the time-shifting property of the Fourier Transform we know that if we have a Fourier Transform pair \( h(k,n) \leftrightarrow H(j\omega_k,j\omega_n) \), then:
$$ h(k-u,n-v) \leftrightarrow H(j\omega_k,j\omega_n) e^{-j(\omega_k u + j\omega_n v)} $$The magnitude of which, \( \vert H(j\omega_k,j\omega_n) \vert \), is unaffected by translations. This renders our descriptor invariant to scale and rotation by design, provided that we sample densely enough (at the cost of high dimensionality). The main problem of this approach is that it requires large areas, which means that in real scenarios it will suffer from occlusions or background motion. This can be greatly alleviated with segmentation masks, which was the starting point of this work. Combining these two techniques we can obtain descriptors which are strongly invariant and can be computed over any image pixel.
Alternatively, we can apply the Fourier Transform only over scale, to obtain a descriptor invariant to scale but does not discard rotation information, which we refer to as SID-Rot. We can apply segmentation masks following the same procedure as for SIFT.
EXPERIMENTS: Multi-layered motion
Here we show SIFT-flow [1] warps with different descriptors: DSIFT, Scale-Less SIFT (SLS) [5], SID [4] and SSID with 'SoftMask' embeddings. The SSID results correspond to the scale-invariant but rotation-dependent version (i.e. SSID-Rot), as it performs better on images which contain few rotations. Ground truth annotations are overlaid in red when available, and the video stops on these frames for an instant. To evaluate these results numerically we warped the ground truth masks for one image using the flow estimates, and computed the overlap (Dice coefficient) with the mask for the other image. This video is part of the supplemental material for the initial paper submission, and does not correspond exactly with the final results reported in the paper, particularly for DSIFT, as very small patches do reasonably well. Please note that the final version of the paper included experiments on segmentation-aware DSIFT, which also outperformed DSIFT, and that SSID-Rot always outperformed the alternatives.
The left column shows the first image in the sequence (top) and the following ones (bottom). The image on top is warped to the image at the bottom. The second column shows the result for dense SIFT (top) and SLS-PCA (bottom). The third column shows the results for SID-Rot (top) and SSID-Rot (bottom).
Results for a real sequence
EXPERIMENTS: Wide-Baseline Stereo
For this experiment we follow the set-up of Daisy [6]. We discretize 3D space into a given number of layers, match each point on one image to the other image, subject to epipolar constraints and the range of the scene, and store the best match at every depth layer. Finally, we use a global optimization algorithm such as Graph Cuts to obtain a piecewise-smooth estimate. We compare our single-shot SSID descriptor with Daisy's iterative figure/ground mask estimation process, where previous depth estimates are used to compute the masks, which unlike ours are binary. The following figures show the depth estimates corresponding to wide-baseline stereo with Daisy and SSID. We present the results for five iterations of Daisy stereo and for a single iteration of SSID with 'Eigen' embeddings, for five baselines. Note that the SSID results correspond to the scale- and rotation-invariant version of the descriptor, whereas for Daisy we rotate the patch along the epipolar line to enforce rotation invariance, as in [6]. Click on the images for a larger version.
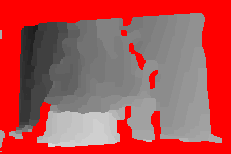
First baseline: images 4 (left) and 3 (right)
Left image, right image, ground truth depth, SID w/ SoftSeg-Pb estimate




Daisy estimates: first to last iteration




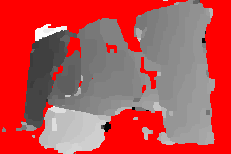
Second baseline: images 5 (left) and 3 (right)
Left image, right image, ground truth depth, SID w/ SoftSeg-Pb estimate




Daisy estimates: first to last iteration





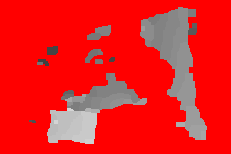
Third baseline: images 6 (left) and 3 (right)
Left image, right image, ground truth depth, SID w/ SoftSeg-Pb estimate




Daisy estimates: first to last iteration




Fourth baseline: images 7 (left) and 3 (right)
Left image, right image, ground truth depth, SID w/ SoftSeg-Pb estimate




Daisy estimates: first to last iteration




Fifth baseline: images 8 (left) and 3 (right)
Left image, right image, ground truth depth, SID w/ SoftSeg-Pb estimate




Daisy estimates: first to last iteration




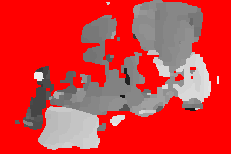
Implementation details:
- 1. For the occlusion cost of Daisy stereo, we use the approach of [6]: a fraction of the maximum cost. We determine its value running the experiment for several values and choosing the one with a better overall performance. Lower occlusion costs result in more conservative estimates for shorter baselines, which introduce less errors on the first step of the iterative process. On the other hand, the initial estimates for the larger baselines contain less data, and converging takes longer (see e.g. the 8-to-3 baseline).
- 2. To determine the best mask, we again use the proposal of [6]. The paper does not mention certain implementation details, such as the area used to determine the fit of each mask. We use a radius of 20 pixels (the grid radius being 15 pixels), and ignore those pixels closer to a disabled grid point than an enabled grid point.
References
- [1] C. Liu, J. Yuen, and A. Torralba. Sift flow: dense correspondence across difference scenes. PAMI, 2011.
- [2] M. Maire, P. Arbelaez, C. Fowlkes, and J. Malik. Using contours to detect and localize junctions in natural images. CVPR 2008.
- [3] M. Leordeanu, R. Sukthankar, and C. Sminchisescu. Efficient closed-form solution to generalized boundary detection. ECCV 2012.
- [4] I. Kokkinos, M. Bronstein, and A. Yuille. Dense Scale-Invariant Descriptors for Images and Surfaces. Technical Report, Ecole Centrale Paris.
- [5] T. Hassner, V. Mayzels, and L. Zelnik-Manor. On SIFTS and their scales. CVPR 2012.
- [6] E. Tola, V. Lepetit, and P. Fua. Daisy: An efficient dense descriptor applied to wide-baseline stereo. PAMI, 2010.