A point is an array of three doubles that represent the X, Y and Z coordinates of the point. Points are used, for instance, to describe leg, traces and landmarks positions. No special point type is defined since it is just a simple array. By its side, transforms are matrix for four rows and four columns. A transform can represent an arbitrary translation or rotation or combinations of them. The type t_transform can be used to define transformation variables.
Some constants are defined to easy the definition and manipulation of points and transforms:
The functions to manipulate transforms are described below.
Returns the identity matrix:
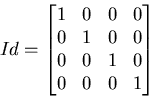
Sets td equal to to: td ![]() to.
to.
Returns a matrix that represents a translation along the X axis:
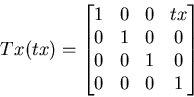
Returns a matrix that represents a translation along the Y axis:
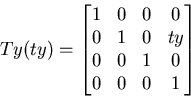
Returns a matrix that represents a translation along the Z axis:
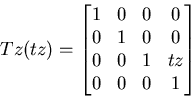
Returns a matrix that represents a translation along axes X, Y, and Z:
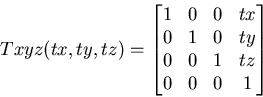
Returns a matrix that represents a rotation around the X axis:
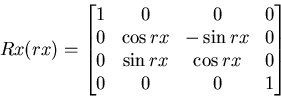
Returns a matrix that represents a rotation around the Y axis:
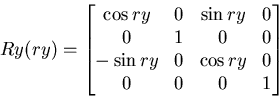
Returns a matrix that represents a rotation around the Y axis:
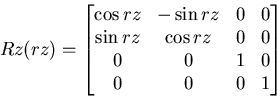
Returns
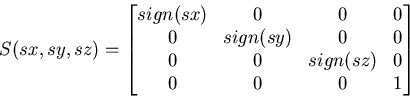
Returns a transform to perform a movement in the given dof of R3 of size v. This function is just a high level interface to call the trs_tx, trs_ty, trs_tz, trs_rx, trs_ry, and trs_rz routines described before.
Performs the product of two transformations: t3 ![]() t1 t2. The effect of
the transform t3 is the concatenation of the effects of t2 and t1 (in this
order).
t1 t2. The effect of
the transform t3 is the concatenation of the effects of t2 and t1 (in this
order).
Adds two transformations: t3 ![]() t1 + t2.
t1 + t2.
Returns the transpose of a transformation matrix: tt ![]() tT.
This function is specially useful since
graphical packages uses transformations matrix that are the transposed of the matrixes as defined
here.
tT.
This function is specially useful since
graphical packages uses transformations matrix that are the transposed of the matrixes as defined
here.
Returns the inverse of a transformation matrix: ti ![]() t-1.
t-1.
Performs the product:
![]()
The above described sequential combination of transformations (CS) apply a given transformation on the frame of reference resulting from the already applied movements. This can result problematic if all movements have been calculated in parallel, in the same frame of reference. The parallel combination of transformations presented here avoids this problem.
Each transformation t produces a variation vart over a given point p:
![]()
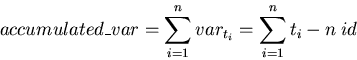
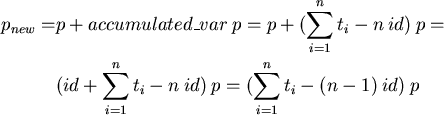
CP=Txyz(tx,ty,tz)+Rx(rx)+Ry(ry)+Rz(rz)- 3 Id
Performs the product
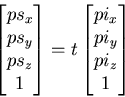
Returns the three first rows of the fourth column of the matrix t. This is equivalent to execute trs_apply(t,<0,0,0>,trans).
Returns the three first rows of the i-th column of the matrix t. This is equivalent to execute trs_apply(t,i,trans) where i has a 1 in the i-th position and zeros in the rest of positions.
Writes the matrix t in the file f.
Writes the transposition of the matrix t in the file f.