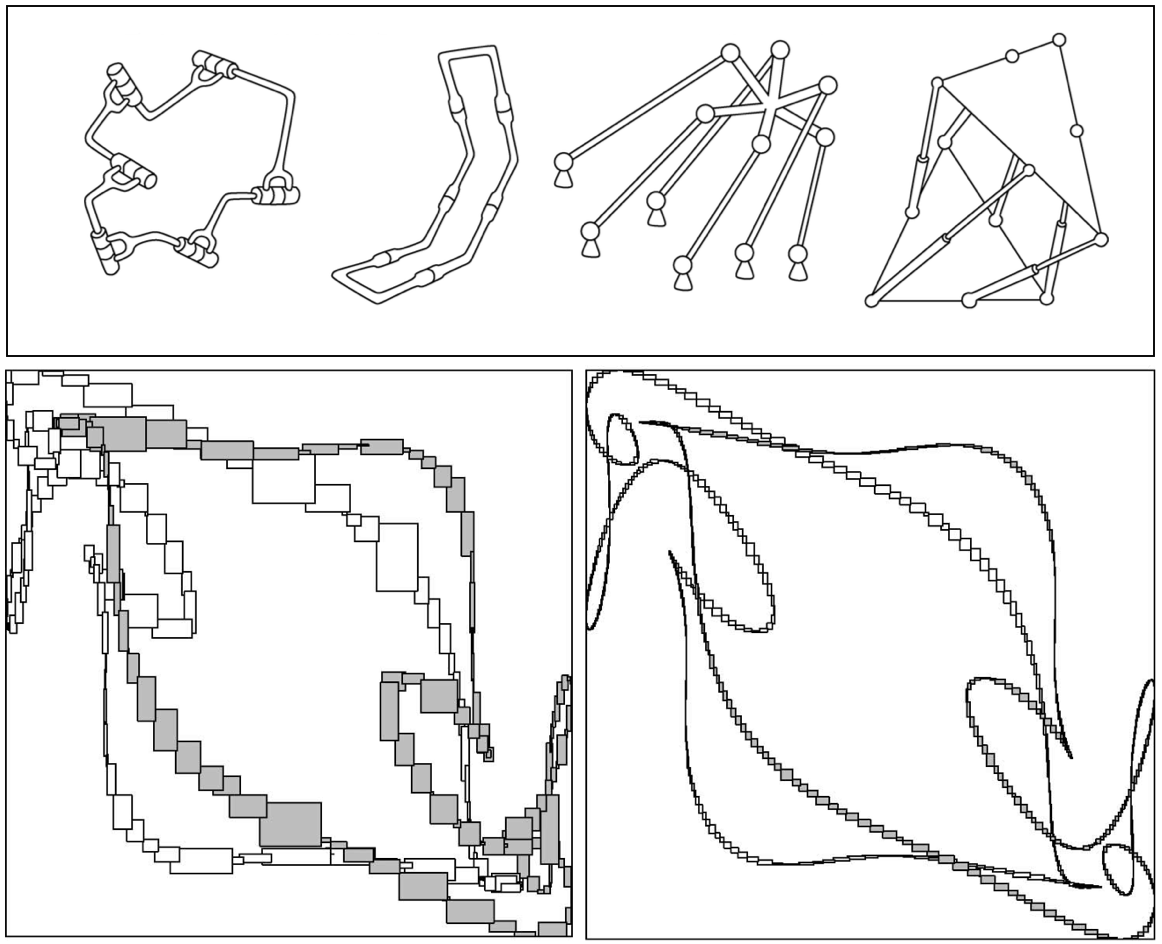
Research interests
My area of
interest is robot kinematics, dynamics, and control. Recently, we
are developing new tools for kinodynamic trajectory planning,
optimization, and control of constrained
multibody systems. Over
the years, I've been also designing algorithms for computing
singularities and workspaces, and for planning
collision and singularity-free paths between given
configurations. Most of such algorithms are
implemented in the
CUIK Suite. During my Ph.D. and
postdoc periods I worked on scene reconstruction and
uncertainty manipulation. The links below provide more
information about these topics.
Kinodynamic
motion planning and control - cable-driven robots -
singularity
analysis - singularity-free
path planning - workspace
determination - grasp synthesis
- position
analysis - molecular
motions - uncertainty
manipulation - scene
reconstruction
Kinodynamic
motion planning and control of closed-chain systems
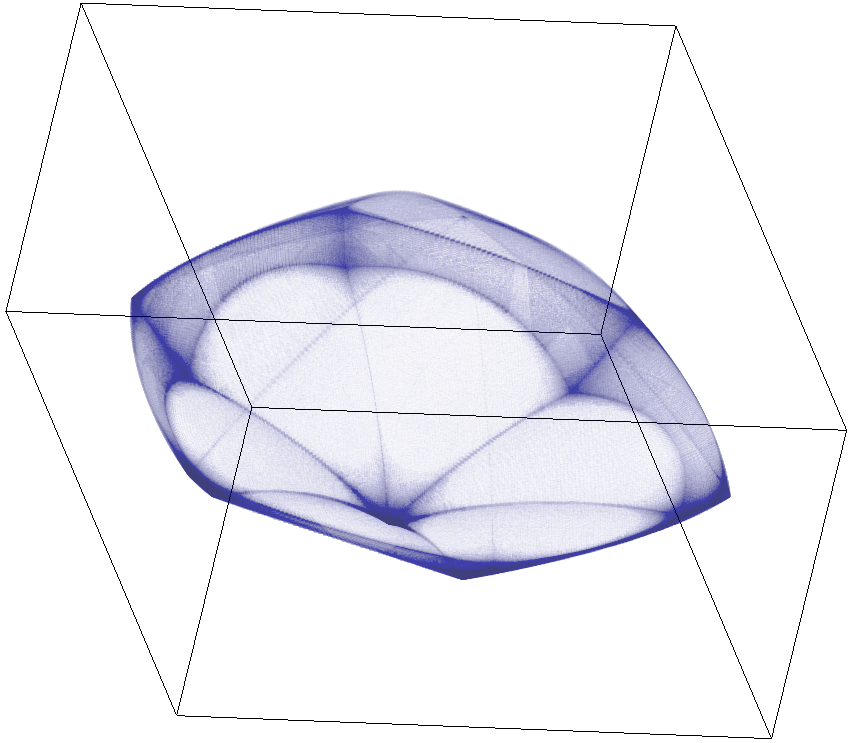
Recently, we are
working on kinodynamic planning and control with dynamic
constraints. By these constraints we mean the
equations of motion of the robot (differential algebraic
equations) and existing limits in the actuation and
constraint forces (inequality constraints). If
necessary, we
can also deal with singularity-avoidance constraints.
For example, the figure above shows the results of
planning a weight-throwing task on a 5-bar parallel
robot. Note how the robot swings back and forth to gain
momentum while avoiding the red locus of singularities
until it finally throws the load (the locus changes when
one of the arm shifts from elbow up to elbow down, or
viceversa). In parallel, we are developing LQR
controllers to stabilize the planned trajectories.
Interestingly, we have shown that one can control a
parallel robot across (or even at) a forward
singularity. Each planning strategy (either avoiding or
allowing the traversal of forward singularities) has its
advantages and shortcomings.
Cable-driven
robots

Motion paths of
cable-driven hexapods must carefully be planned to
ensure that the lengths and tensions of all cables
remain within acceptable limits, for a given wrench
applied to the platform. The cables cannot go slack (to
keep the control of the robot) nor excessively tight (to
prevent cable breakage) even in the presence of bounded
perturbations of the wrench. Our work has been on developing a path planner
that respects such tension constraints, and at the
same time avoids eventual obstacles in the
workspace. The planner can be used to
navigate the full 6D C-space or smaller subspaces
defined by contact or geometric constraints. More
information can be found in our 2016
paper in the IEEE TRO. We have also given a
variant of the technique for aerial-towed
cable systems (aka the "FLYCRANE").
Singularity
analysis

Singularity analysis is a central
topic of robot kinematics. It has as a goal the study
of certain configurations, termed singular or
critical, where important changes take place in
the kinetostatic performance of a mechanism. Rigidity
or dexterity losses arise, and there may appear
unresolvable or uncontrollable end-effector forces,
among other effects. Obtaining complete maps of the
singularity locus is thus essential for a proper
robot design. We have developed an extensive theory
and algorithms for computing all singularity loci of a
mechanism. A distinctive feature of the methods is that they
are applicable to non-redundant mechanisms
of general architecture. See our papers in the
2008-2015
period (a
good start is MMT
2013). Our 2016 book presents
all such results in a consistent manner.
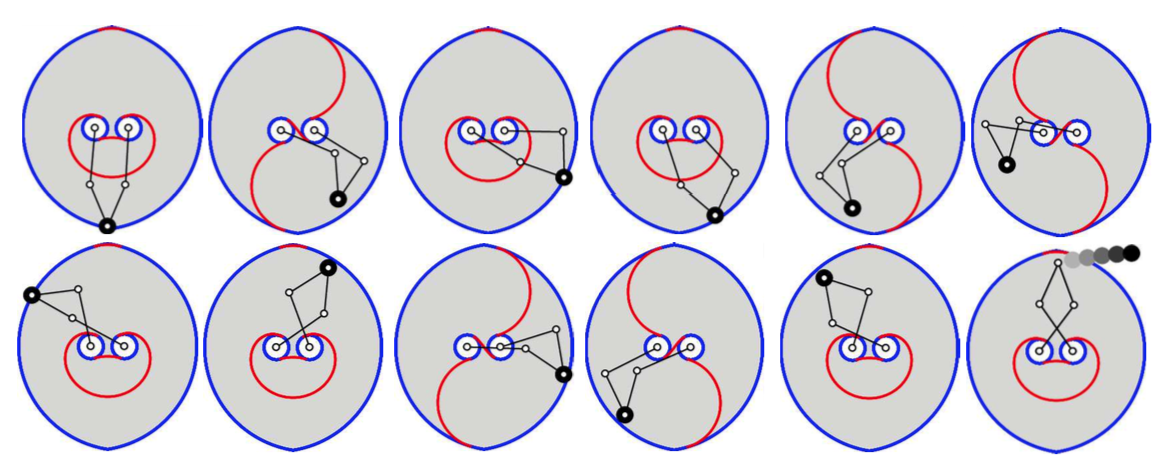
Singularity-free
path planning

Here we have
shown how it is possible to send forward or inverse
singularities to infinity, obtaining an algebraic
formulation of the singularity-free C-space of a
mechanism. C-space singularities are sent to infinity
too, which results in a nicely smooth configuration
space. This allows us to define a conceptually simple
higher-dimensional continuation strategy to find paths
between given configurations. Since the C-space is
smooth, it can be navigated without fear of finding
bifurcations. This results in an automated method for
computing singularity-free paths in general
non-redundant mechanisms. These results can be found
in our 2013
IEEE TRO paper and in our 2016 book.
The approach has also been validated
empirically on the 3-RRR robot of the picture above.
Molecular
motions
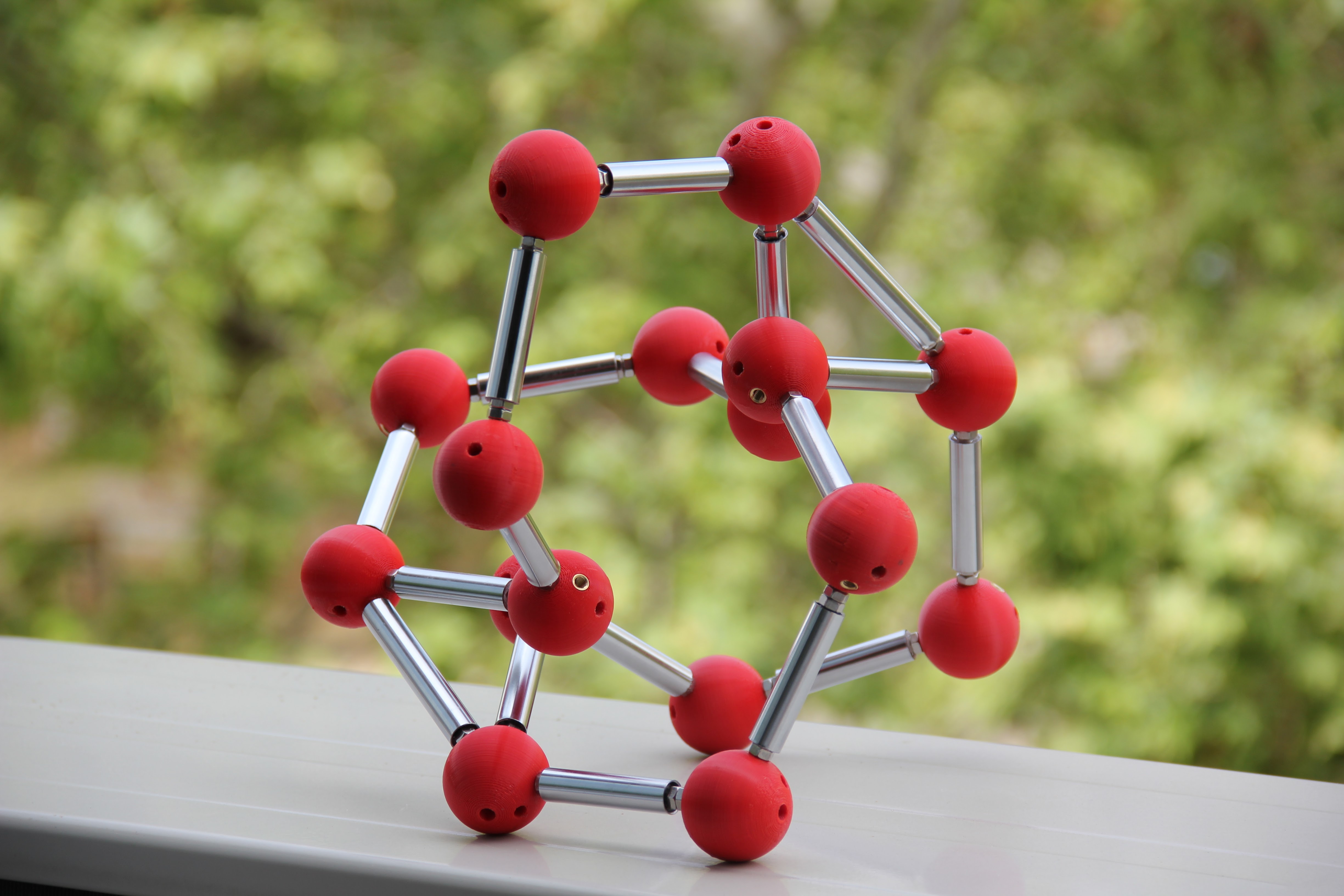
We also have
shown how our algorithms can be applied to explore
the conformational space of biomolecules. We
here advocate for the power of the so-called
rigid-geometry hypothesis, which allows us to model a
molecule's C-space with a reduced number of
configuration coordinates, subject to a system of
kinematic or geometric constraints. We solve such
systems through branch-and-prune or numerical
continuation methods. In colaboration with Adnan
Sljoka, Bernd Schulze, and Walter Whiteley, we have
also explored the C-space
of symmetric molecular linkages.
Position
analysis
This was
our main focus in the period 2005-2010. Our goal was
to find a general solution to the position analysis of
multiloop linkages. I.e., for computing all possible
configurations that a linkage can adopt, while
respecting the kinematic constraints imposed by its
joints. The problem finds applications to robotics
(direct and inverse kinematics of serial/parallel
robots, cooperative manipulation, and closed-chain
motion planning), structural biology (conformational
analysis of biomolecules), multibody dynamics (initial
position and finite displacement problems), and
computer-aided design (variational CAD and assembly
positioning). Main papers are ASME
2007 and TRO
2009, or, through an alternative approach, MMT2012.
Grasp
synthesis
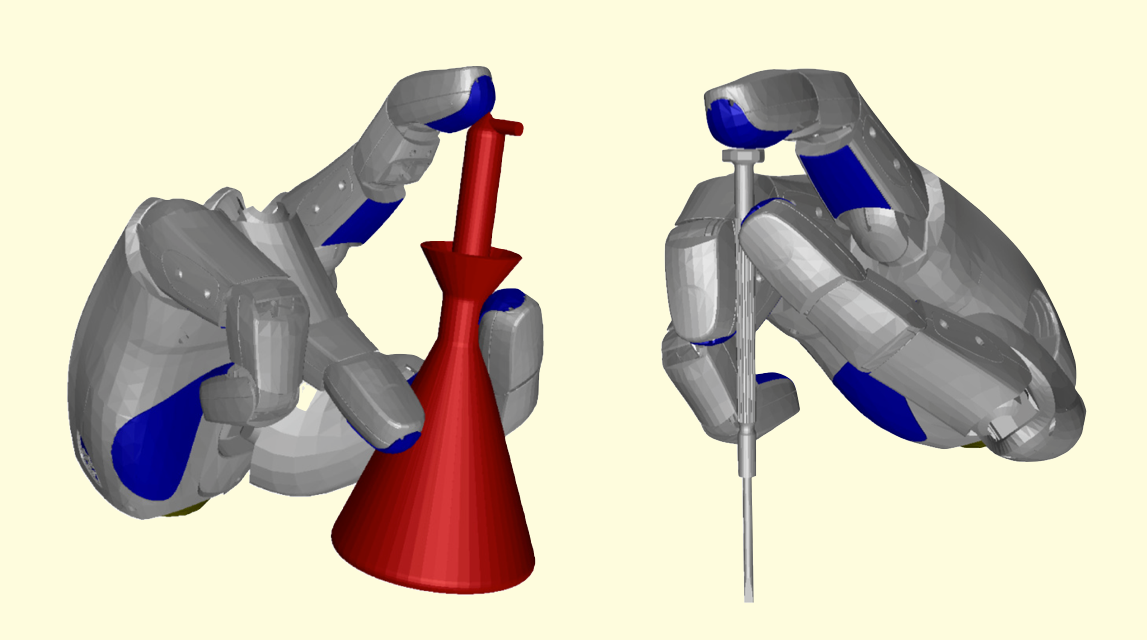
Several
aspects have to be addressed before realizing the
dream of a robotic hand-arm system with human-like
capabilities, ranging from the consolidation of a
proper mechatronic design, to the development of
precise, lightweight sensors and actuators, to the
efficient planning and control of the articular forces
and motions required for interaction with the
environment. We have developed algorithms for a main
problem within the latter aspect, known as the grasp
planning problem: Given a robotic system formed by a
multifingered hand attached to an arm, and an object
to be grasped, both with a known geometry and location
in 3-space, determine how the hand-arm system should
be moved without colliding with itself or with the
environment, in order to firmly grasp the object in a
suitable way (defined by task-dependent hand-object
contact constraints). See IJRR
2011, TRO
2013 and the PhD
Thesis by Carlos Rosales.
Workspace
determination
We have developed a new method for workspace boundary
determination on general structure manipulators. The
method uses our branch-and-prune technique to isolate a
set of output singularities. Then, following Haug et
al., we classify the points in this set according to the
motion impediment they give rise to. A detailed map of
the workspace is obtained as a result, where all
interior and exterior regions, together with the
singularity or barrier sets that separate them, get
clearly identified. The method can deal with open- or
closed-chain robots, whether planar or spatial, and is
able to take joint limits into account. Advantages over
previous methods based on continuation include the
ability to converge to all boundary points, and the fact
that a priori knowledge of the workspace is not
required. See TRO
2012, ASME
2013, and Chapter 4 of this
book.
Uncertainty
manipulation
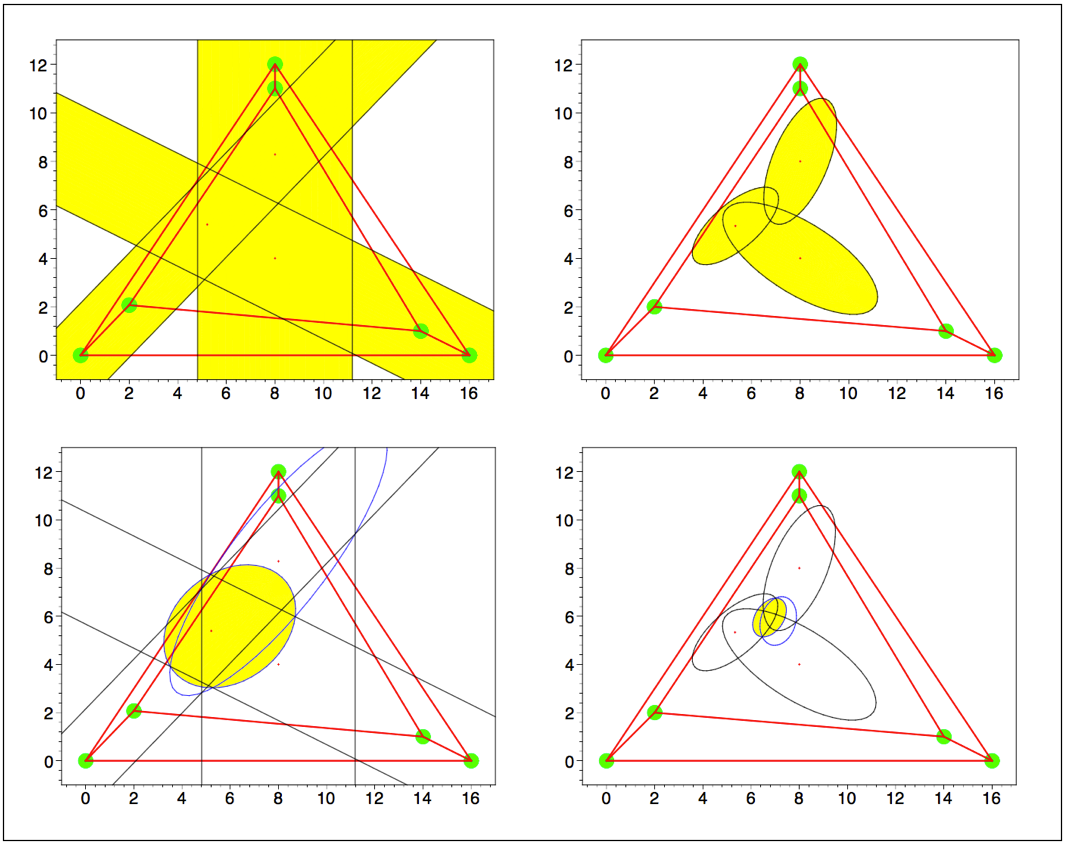
In the real world, the
need to cope with uncertainty arises at all levels of
a robot task, during sensory perception, object
representation, or task execution. In collaboration
with other members of the KRD group, we have developed
methods for handling such uncertainty, including
general-purpose tools like the
Ellipsoidal Calculus Toolbox, or specific
methods for error
estimation in trilateration and pose
estimation devices.
Scene
reconstruction from line drawings
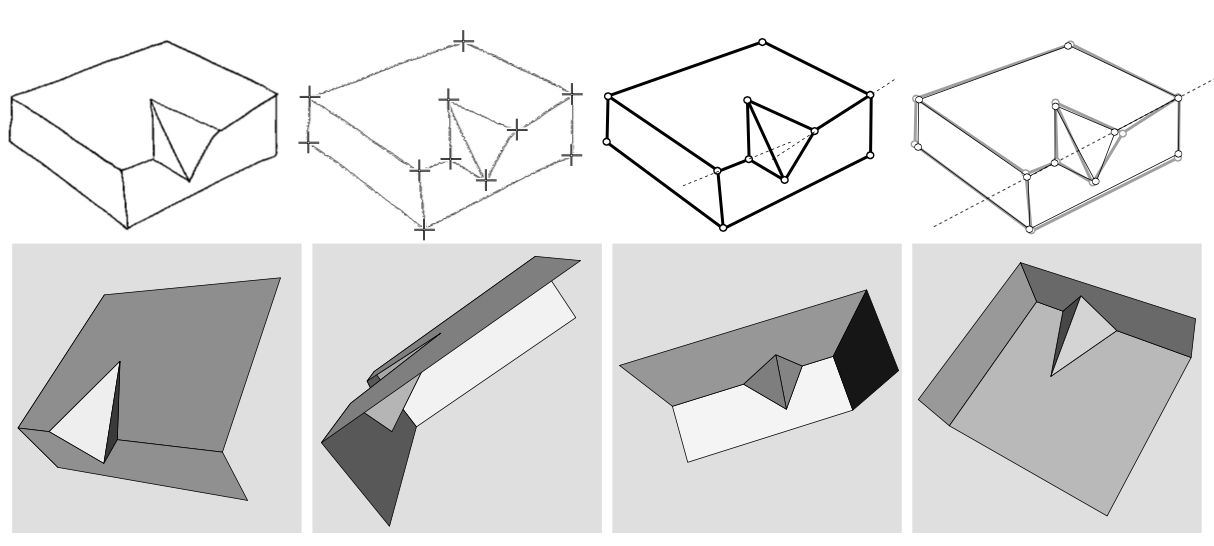
During my PhD I worked in machine
interpretation of line drawings. This is also
known as the "shape-from-image" problem, where
"image" means a "hand-made sketch" essentially. The
goal was to fully automate the process of converting
one such sketch to the most-plausible
three-dimensional model it represents. The work
studies the polyhedral case, its connections with
rigidity theory, and provides solutions to
implementation problems like image
"superstrictness". Main publications are Ros
and Thomas 2002, Ros
et al. 2003, Ros
and Thomas 2005 and my own PhD
thesis.
|