| Home |
| Publications |
| PhD
Thesis |
Singularity-invariant leg rearrangements in Stewart platforms
PhD advisor : Federico Thomas
Description
The
Stewart-Gough platform was first introduced by E. Gough in 1954 and,
since then, it has been used for many applications thanks to its great
stiffness, accuracy and robustness in comparison with serial
manipulators. It has triggered the research on parallel
manipulators and continues to be the center of many researches
because, despite its simple geometry, its analysis translates into
challenging mathematical problems. One of the most challenging ones is
the geometric interpretation of its singularities, that is, those
positions where the platform loses stiffness. A complete geometric
characterization of these unstable poses is still an open problem.
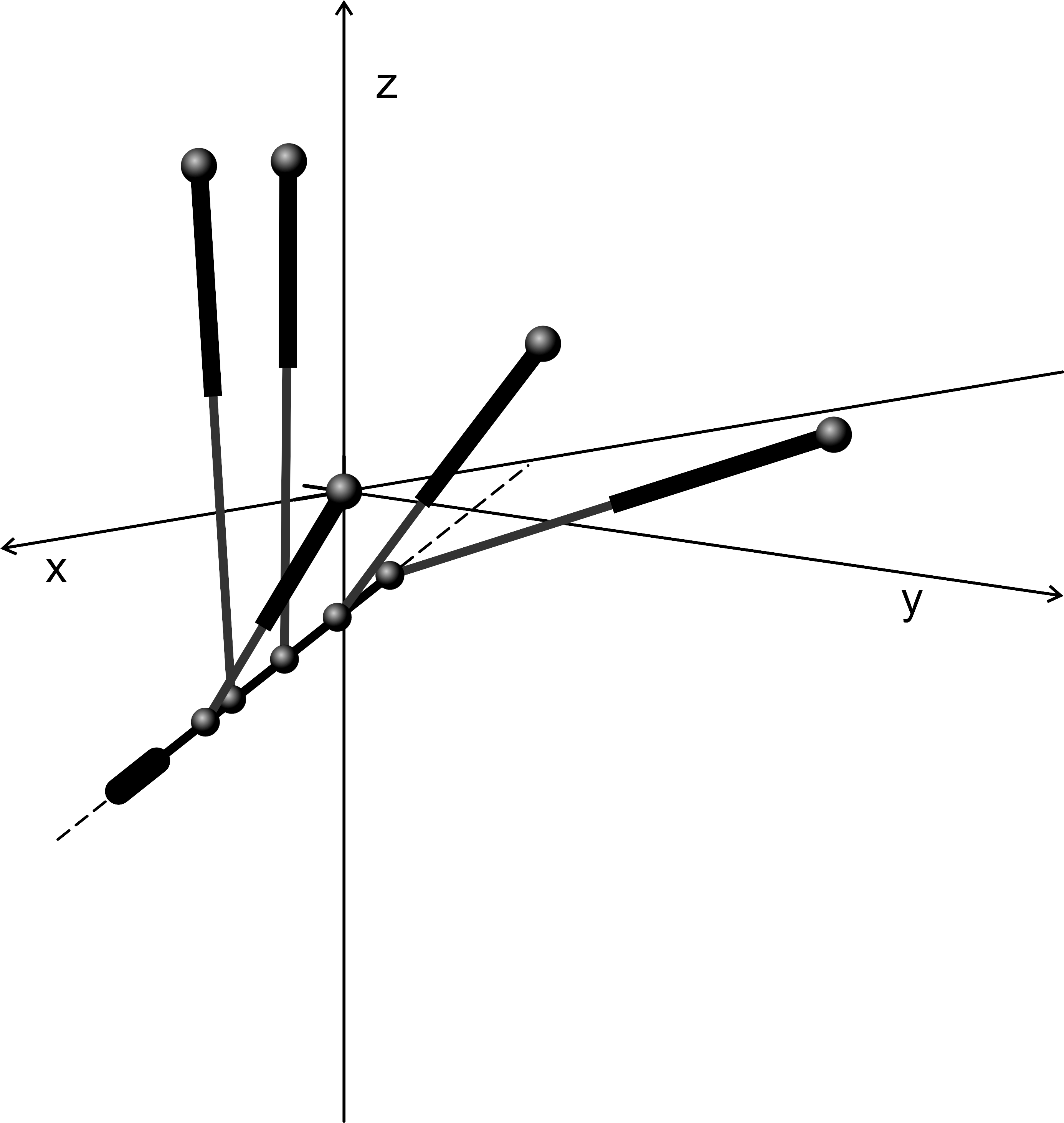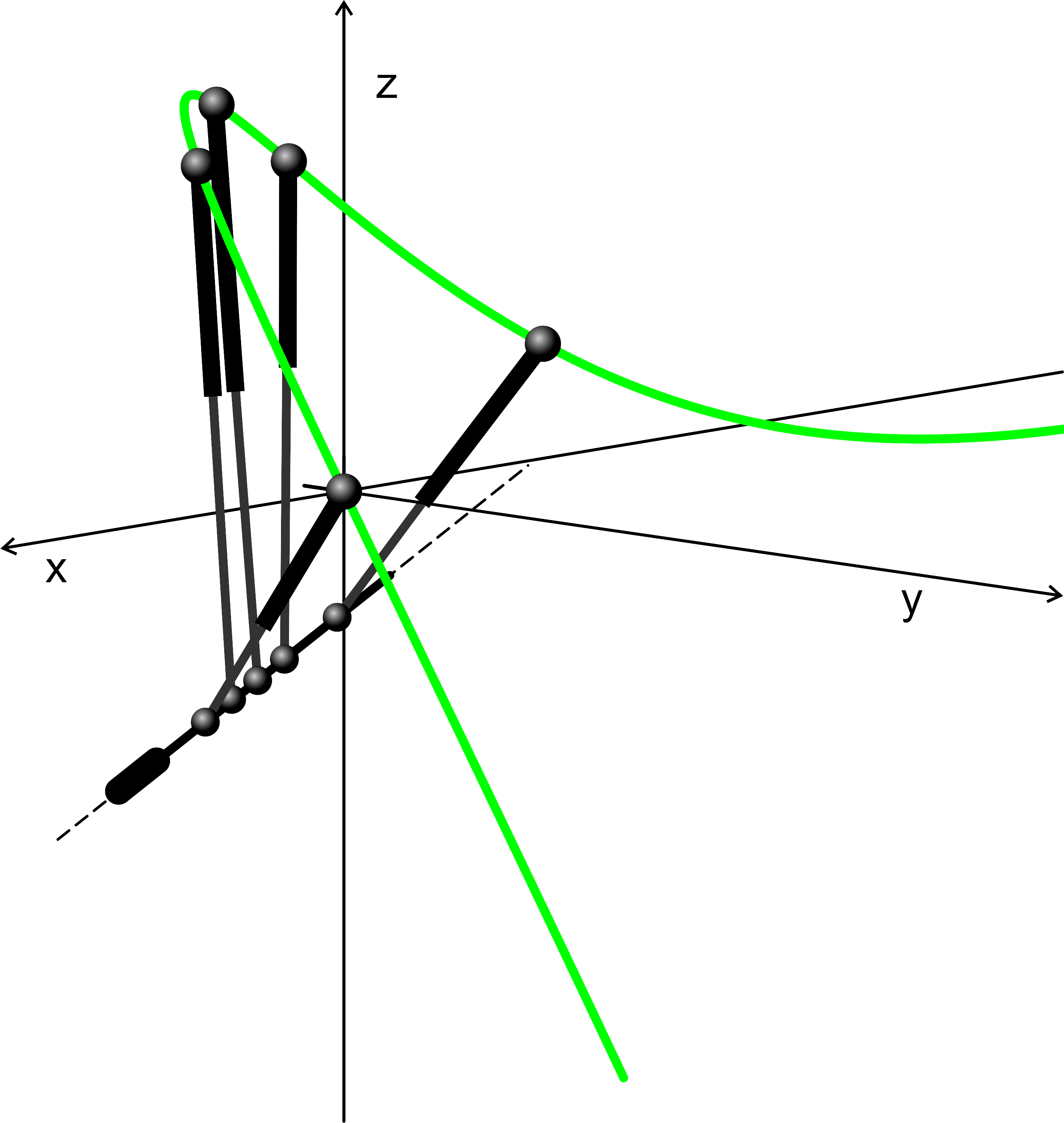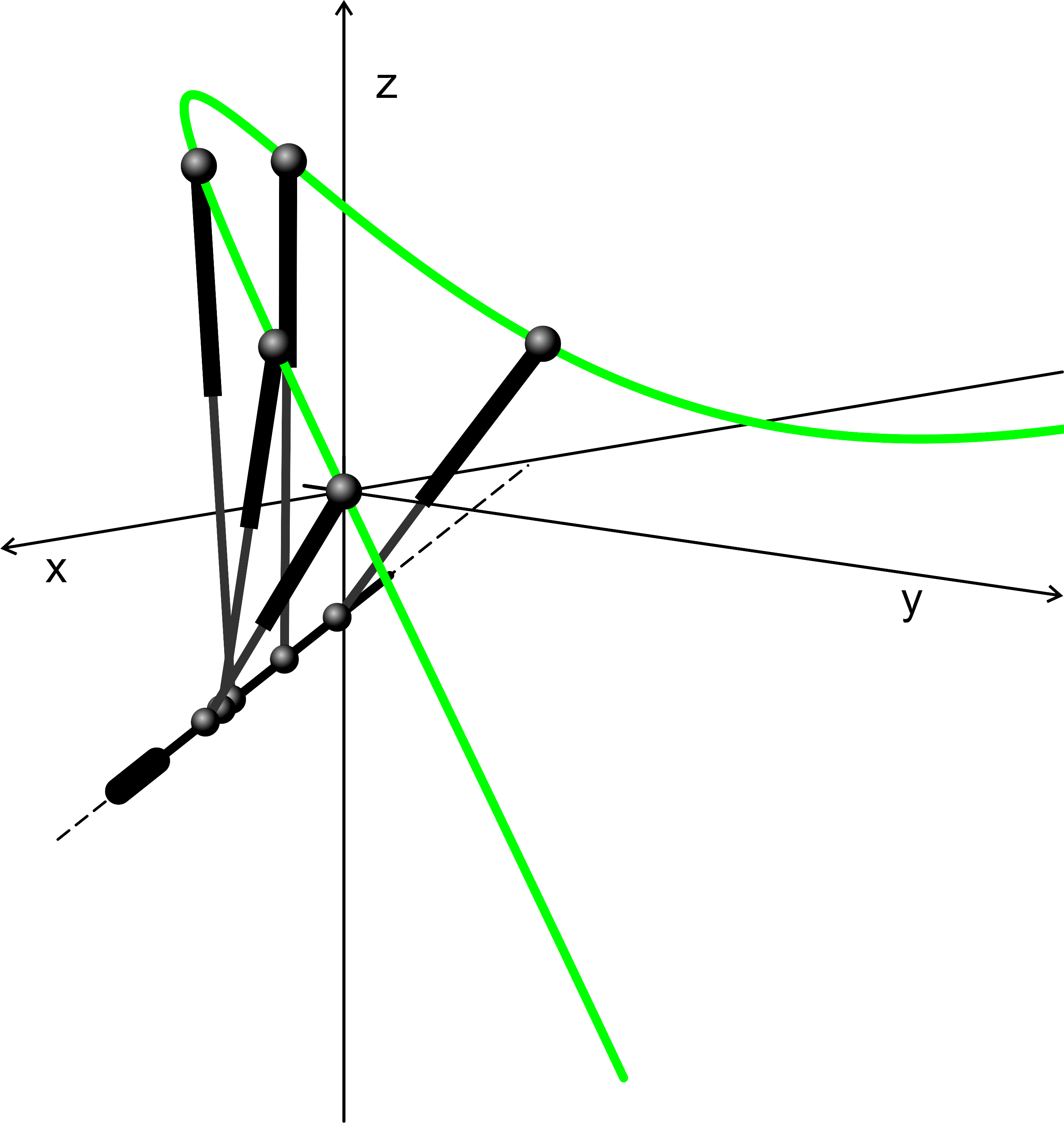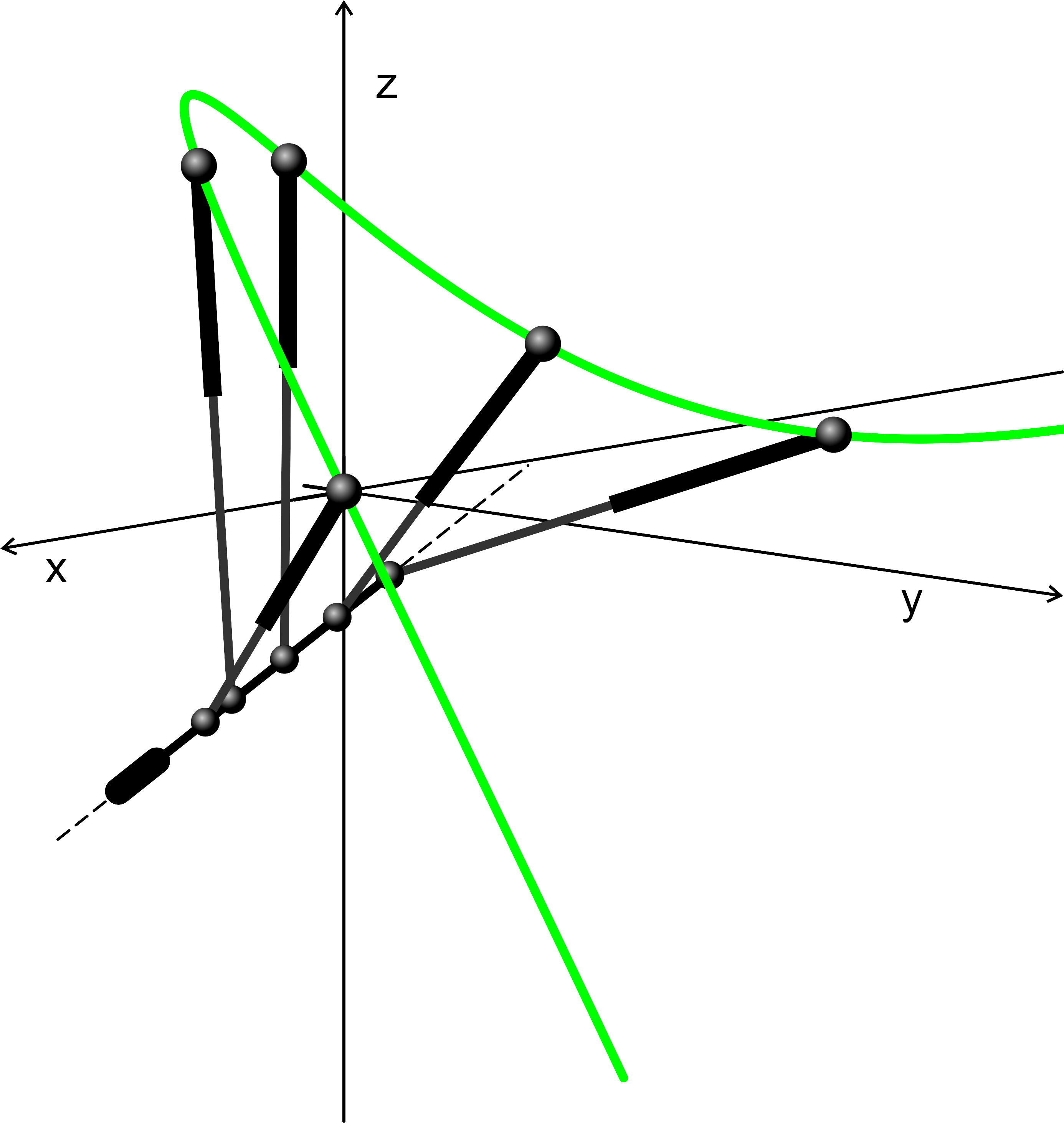
The present thesis provides new insight into this problem from a completely new approach: finding singularity-invariant leg rearrangements.
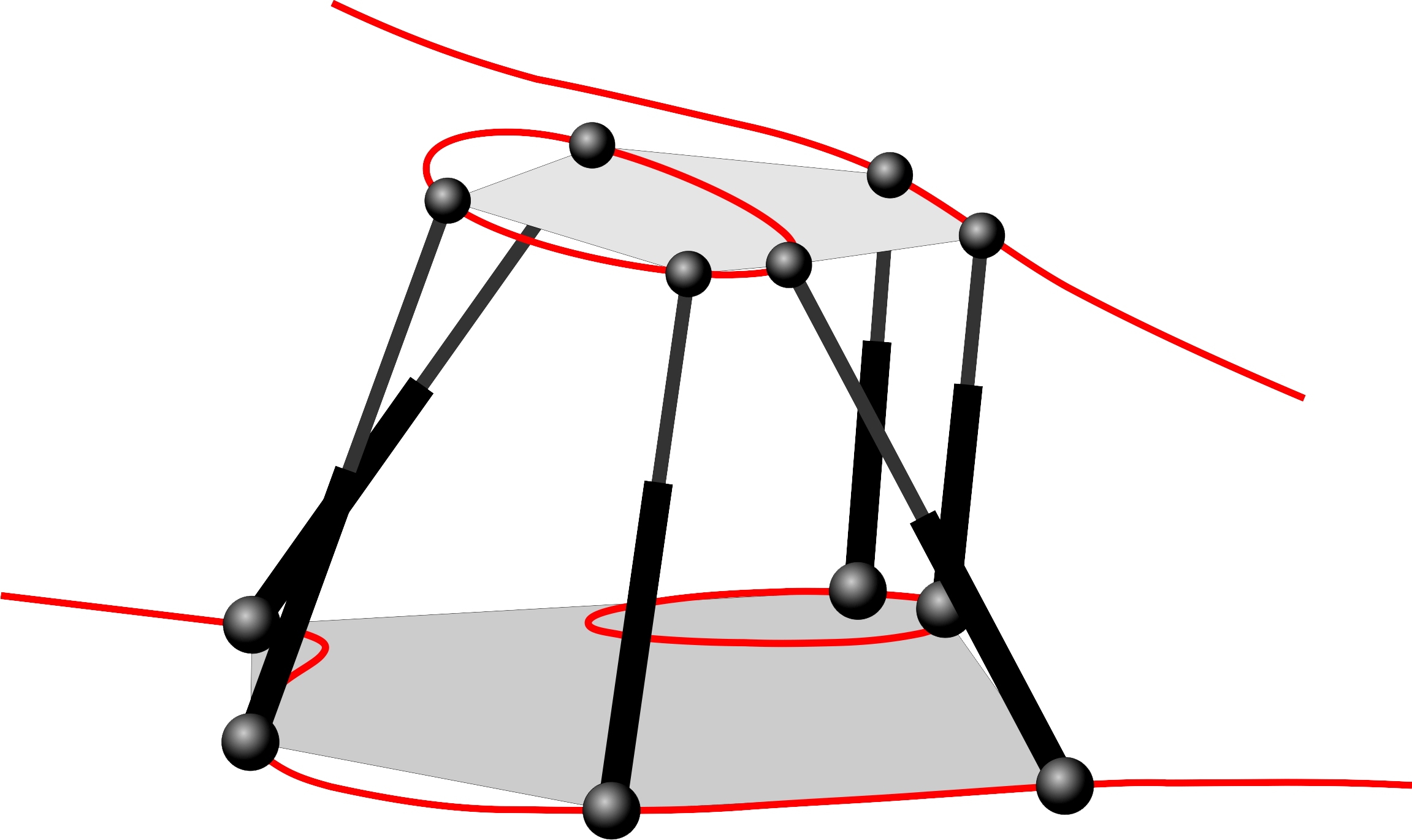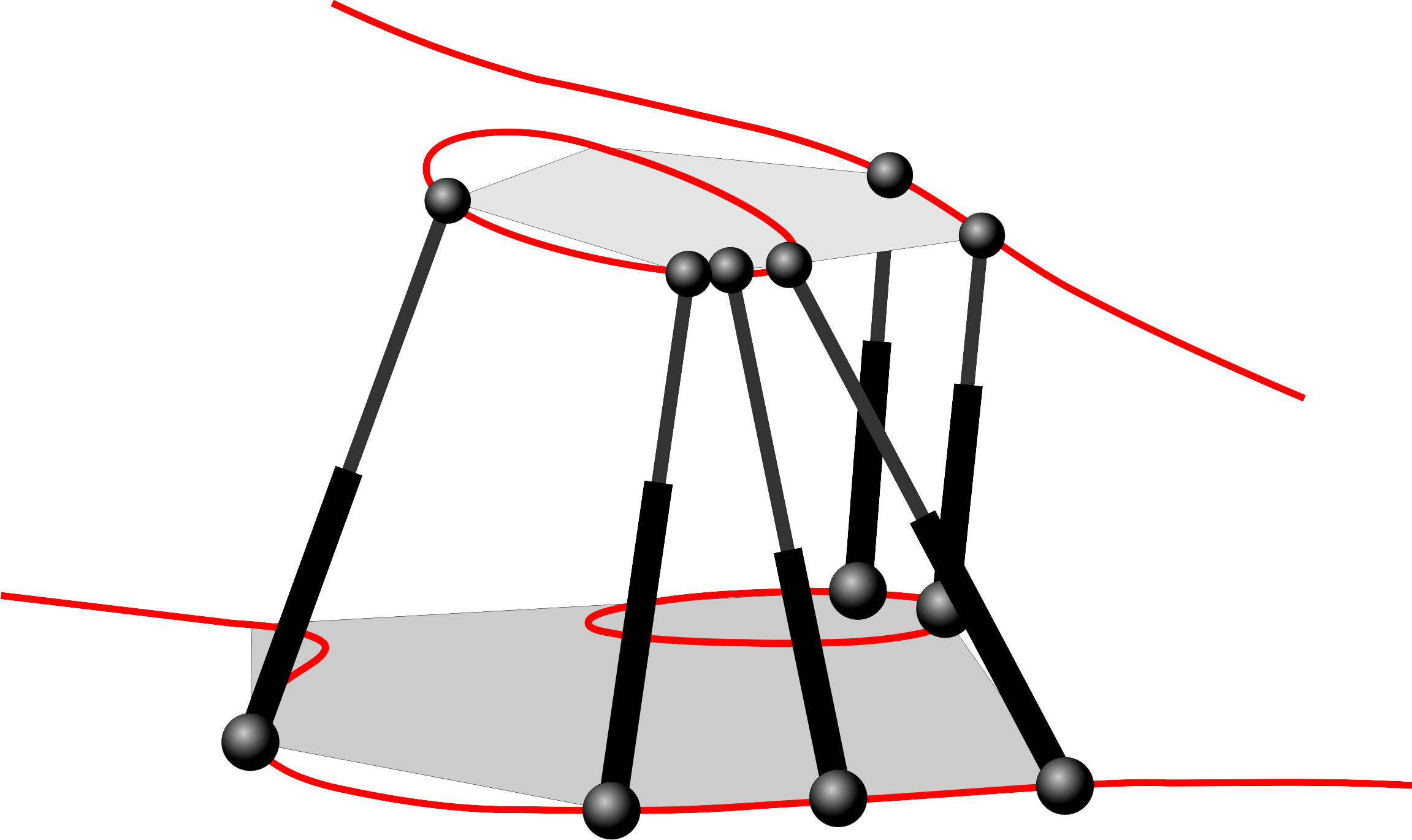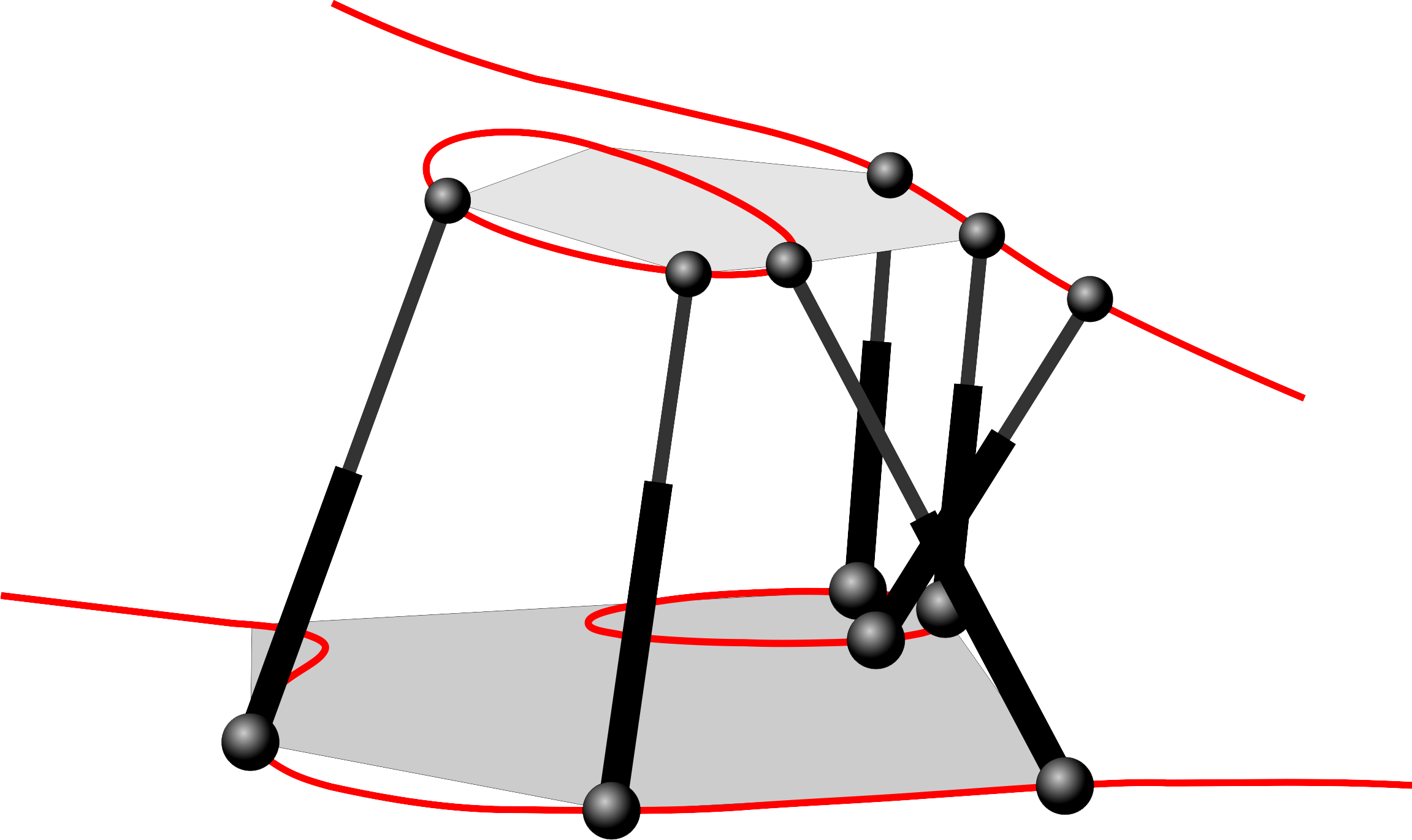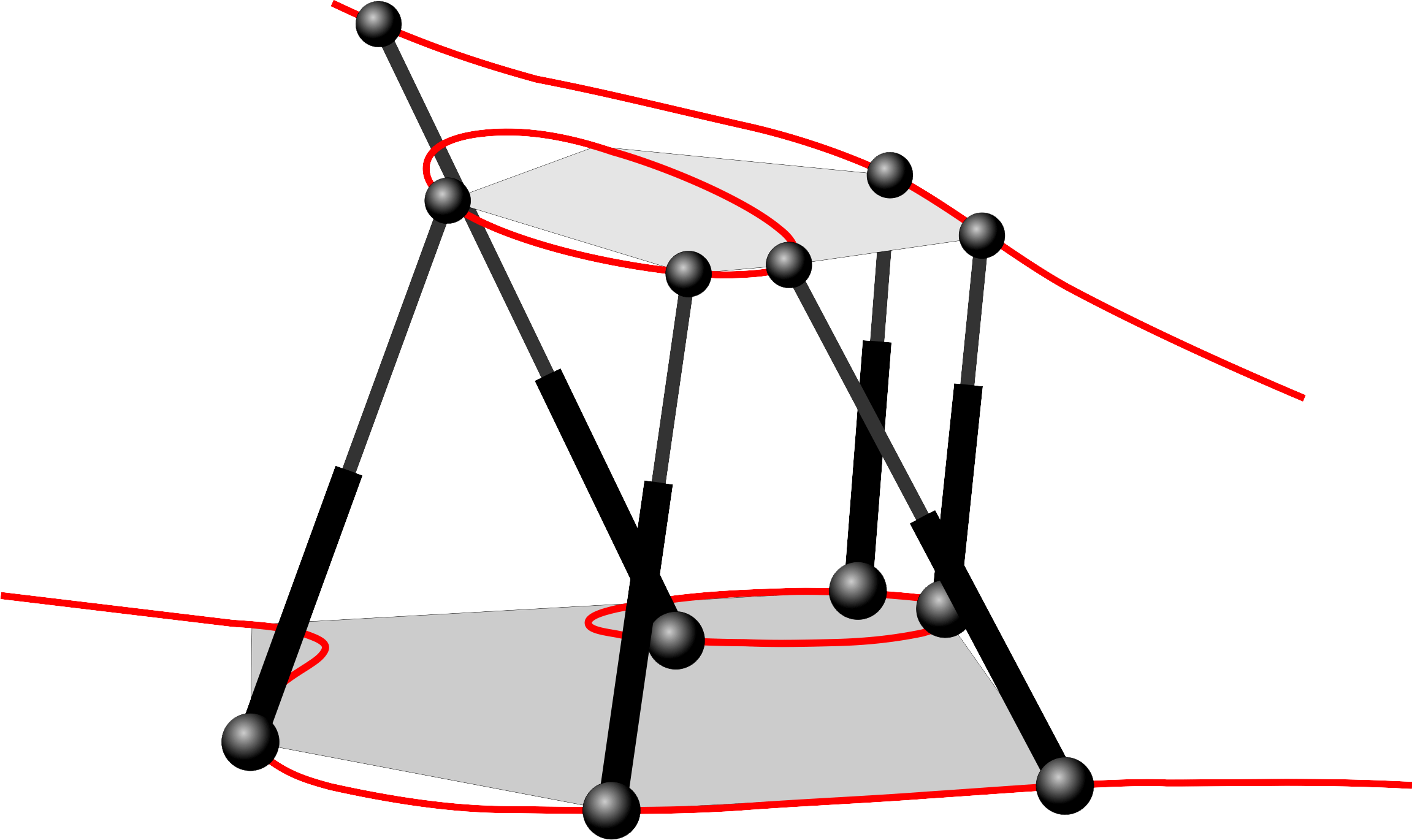
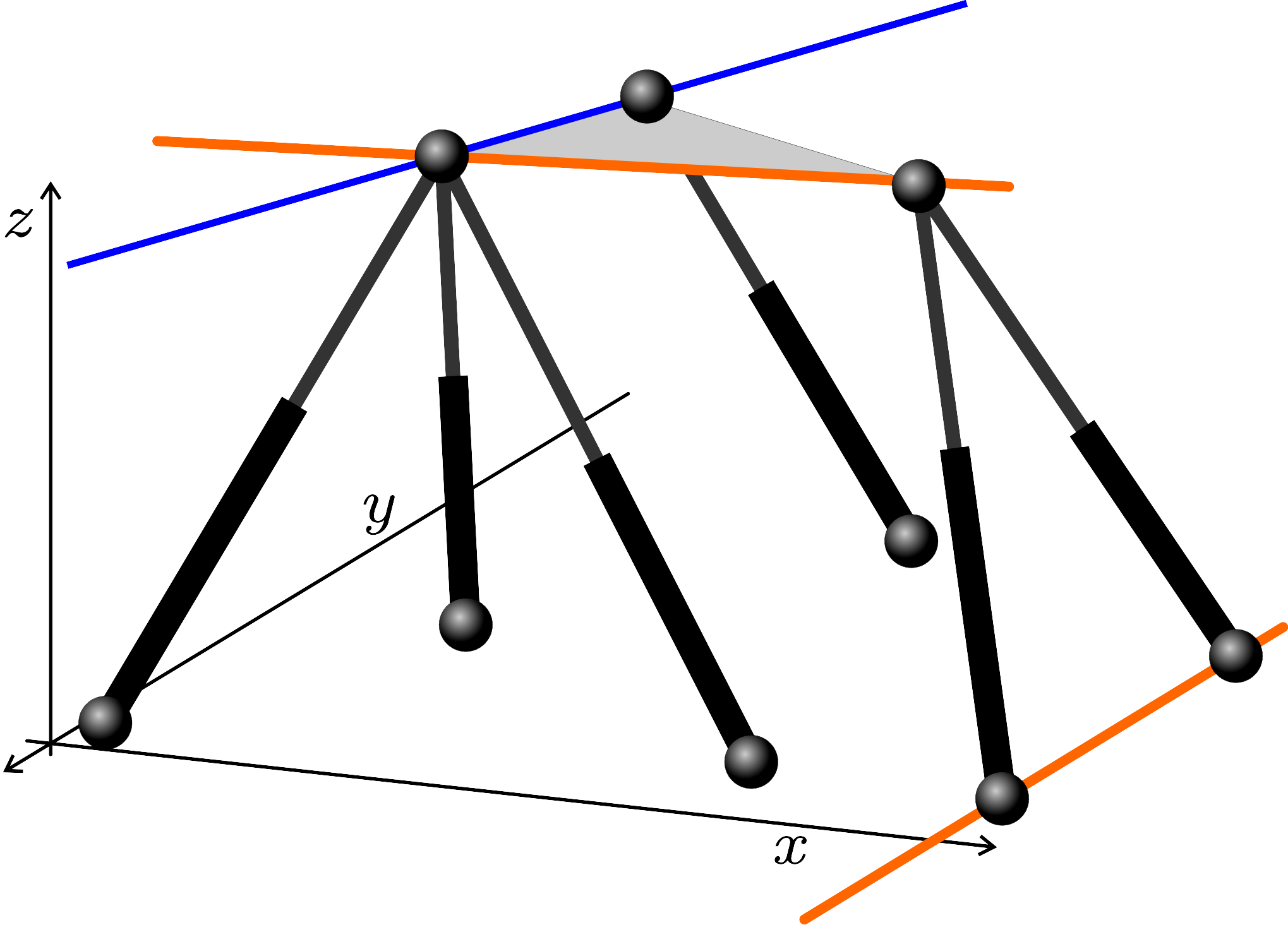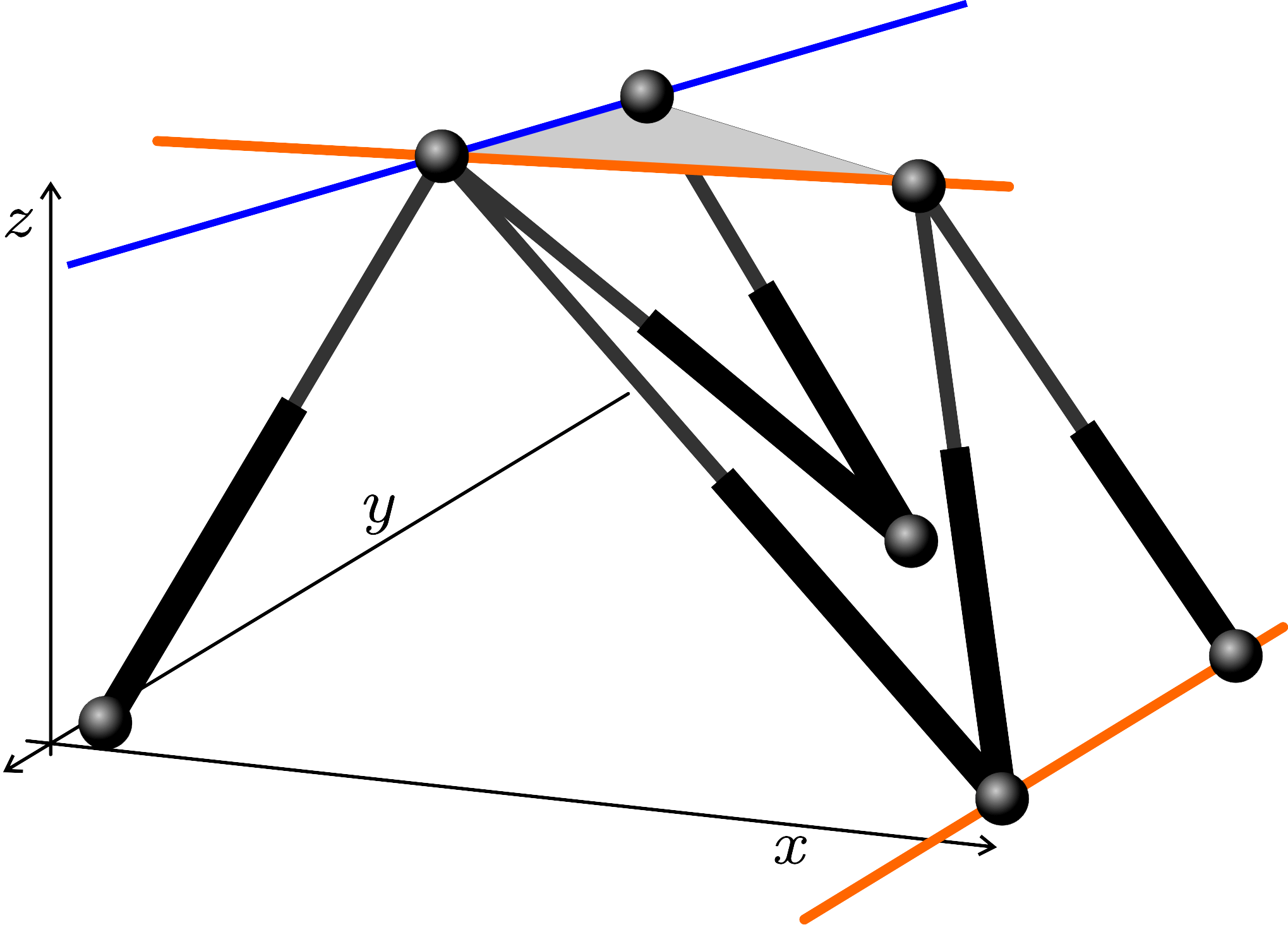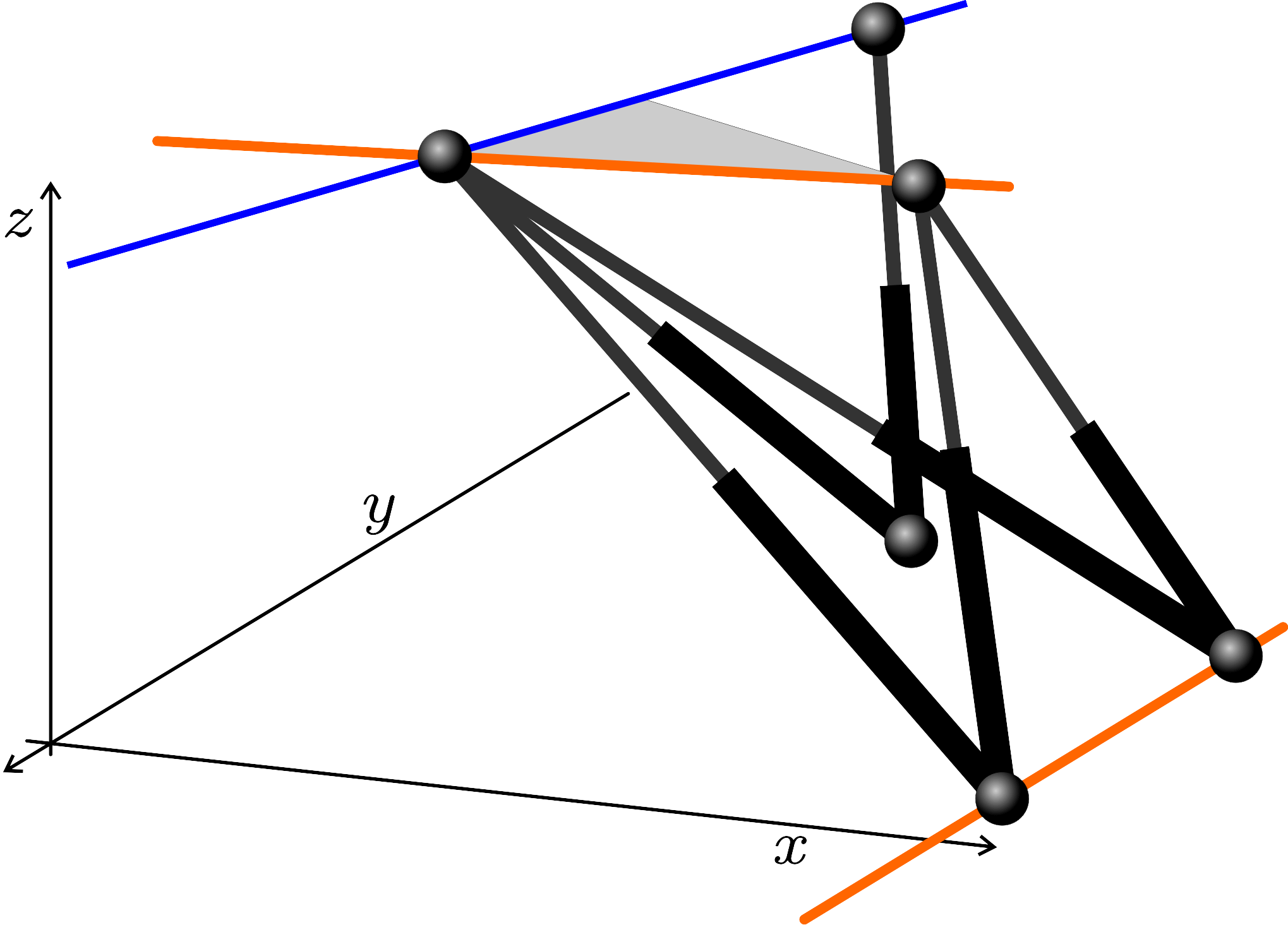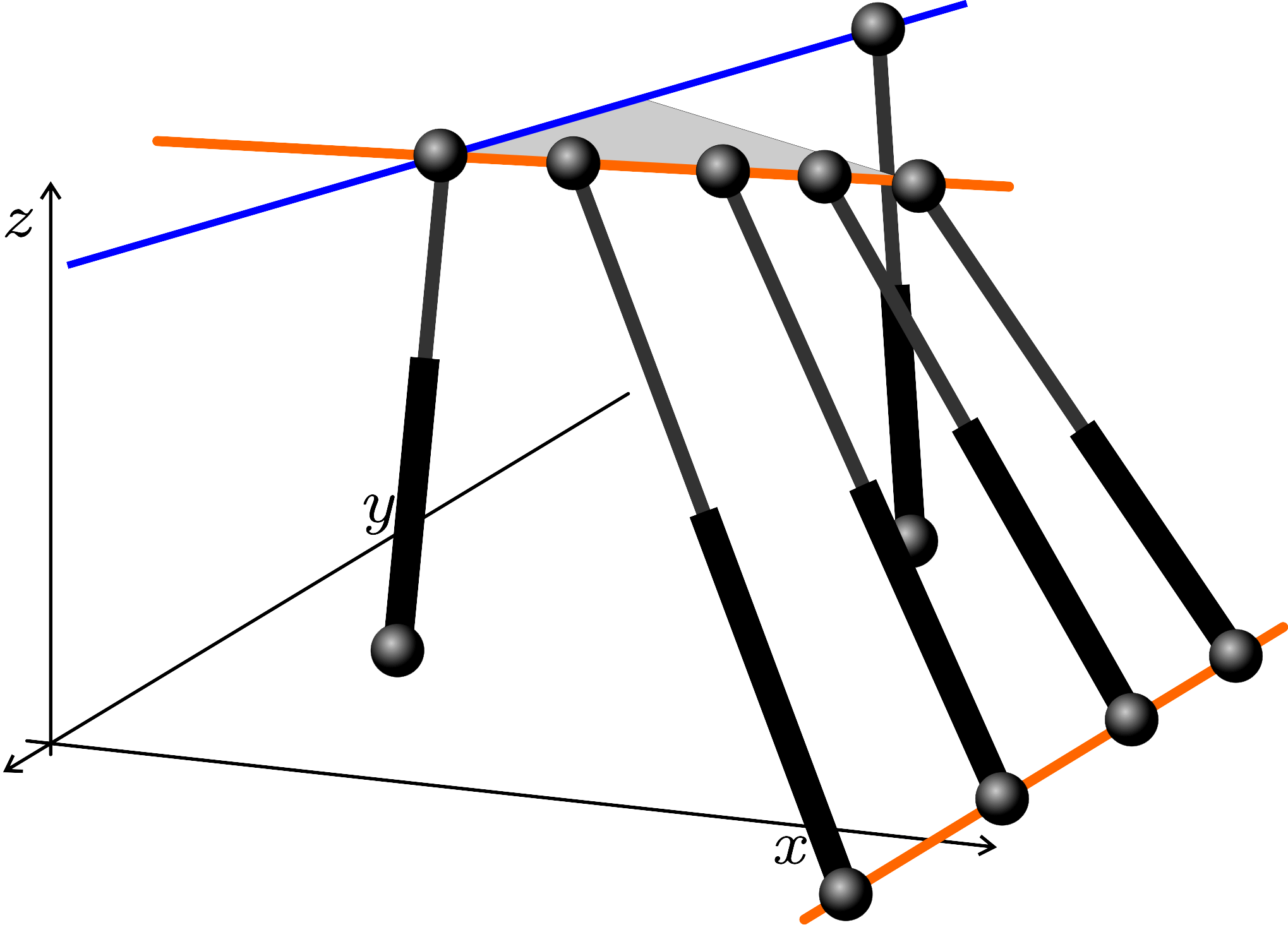
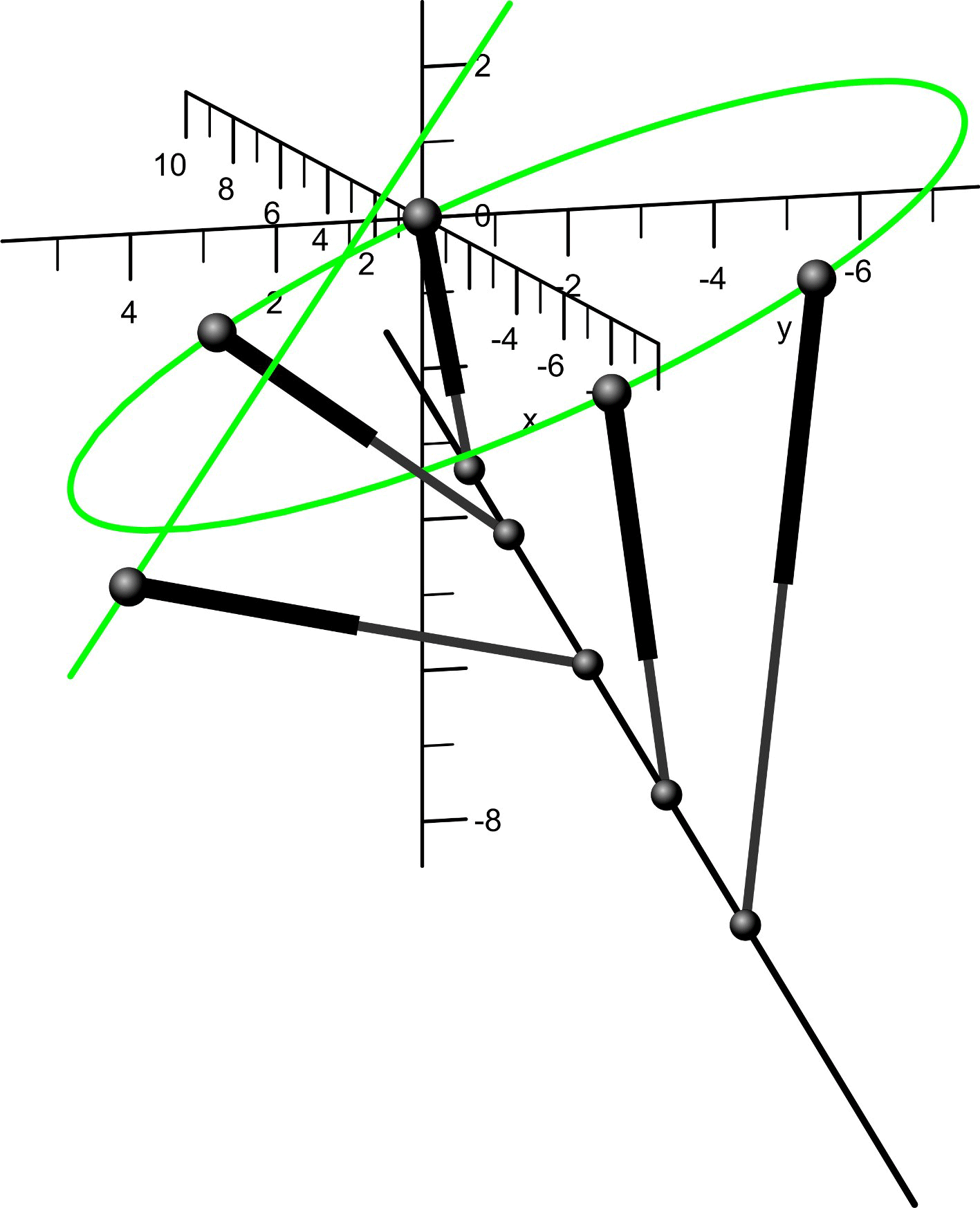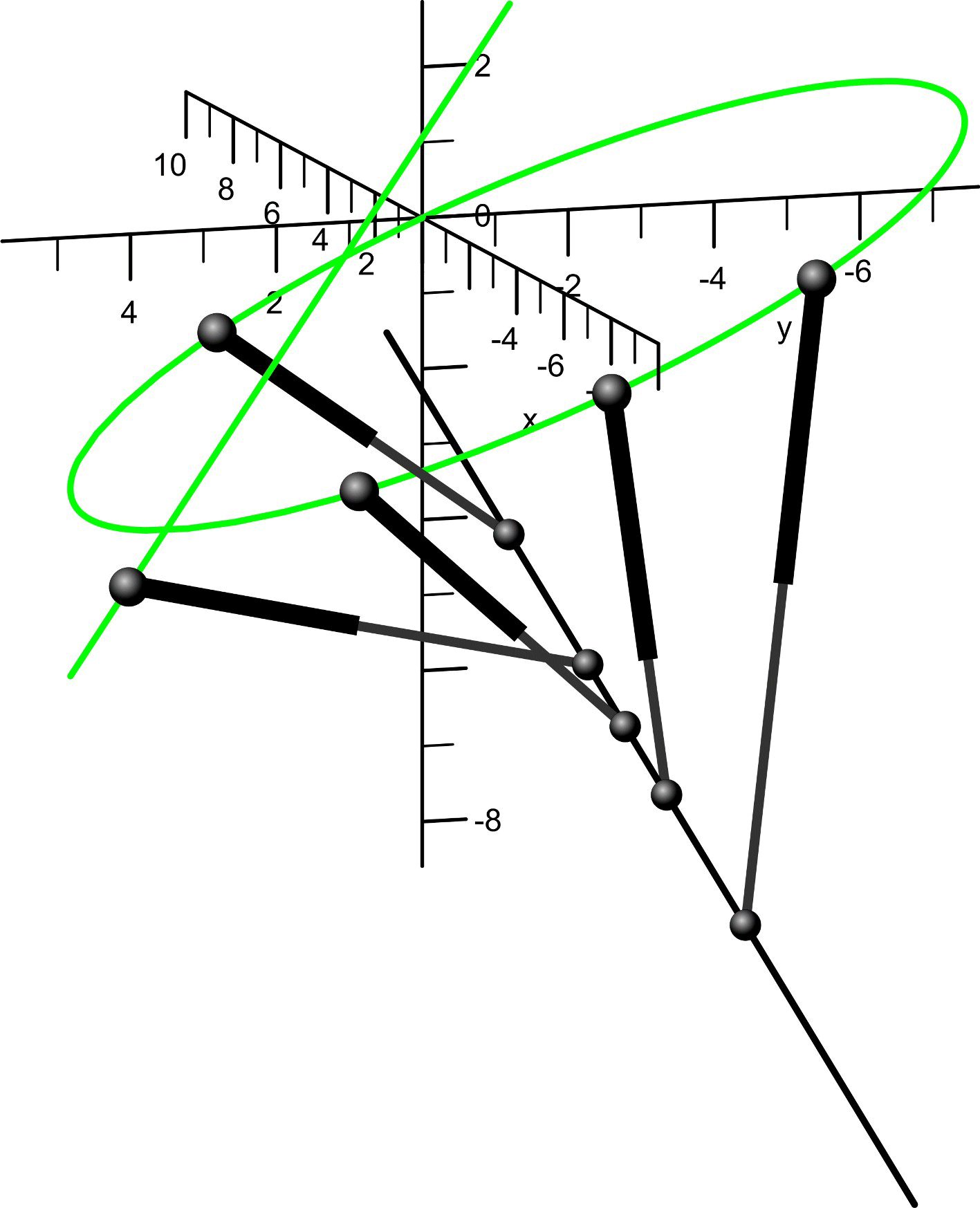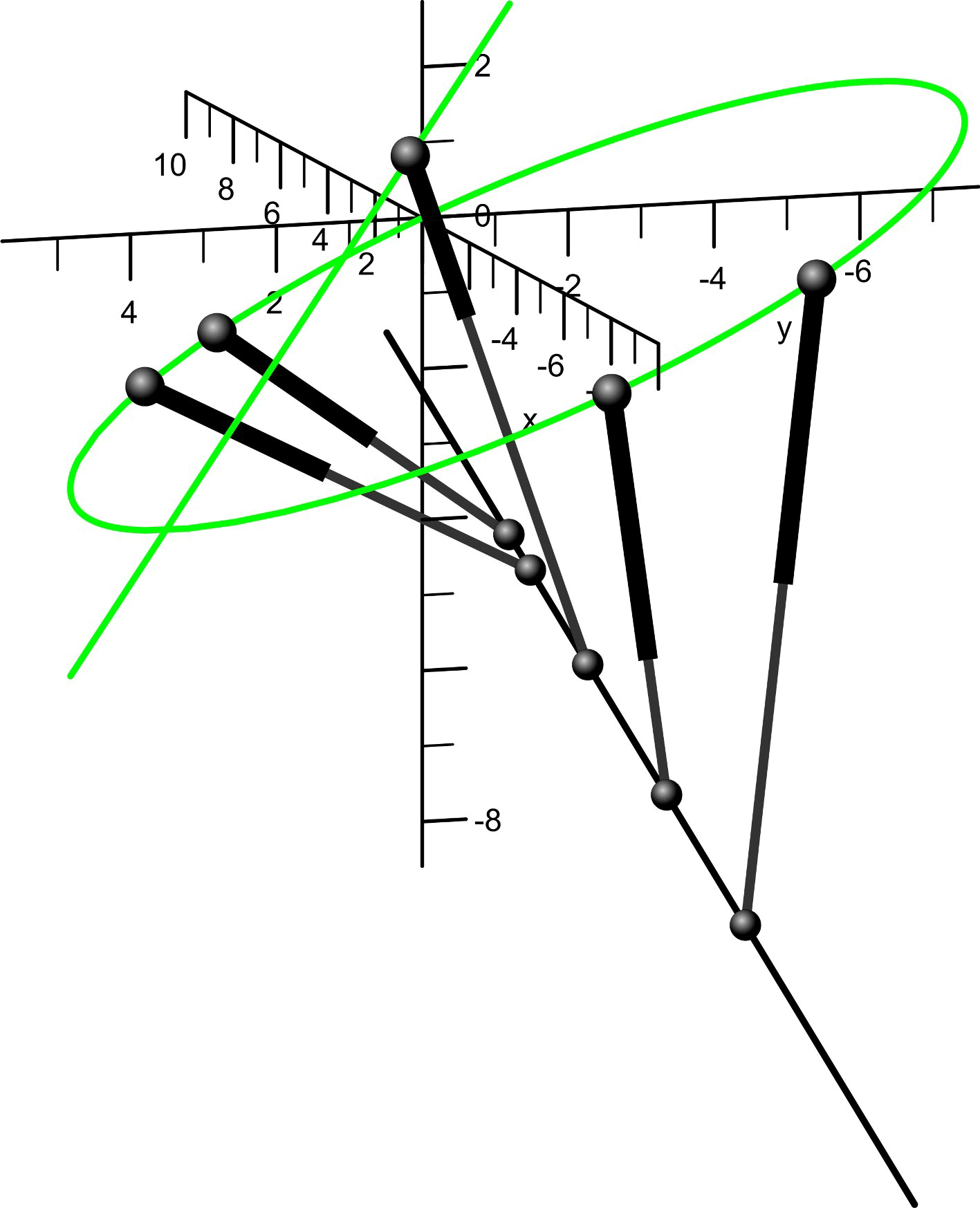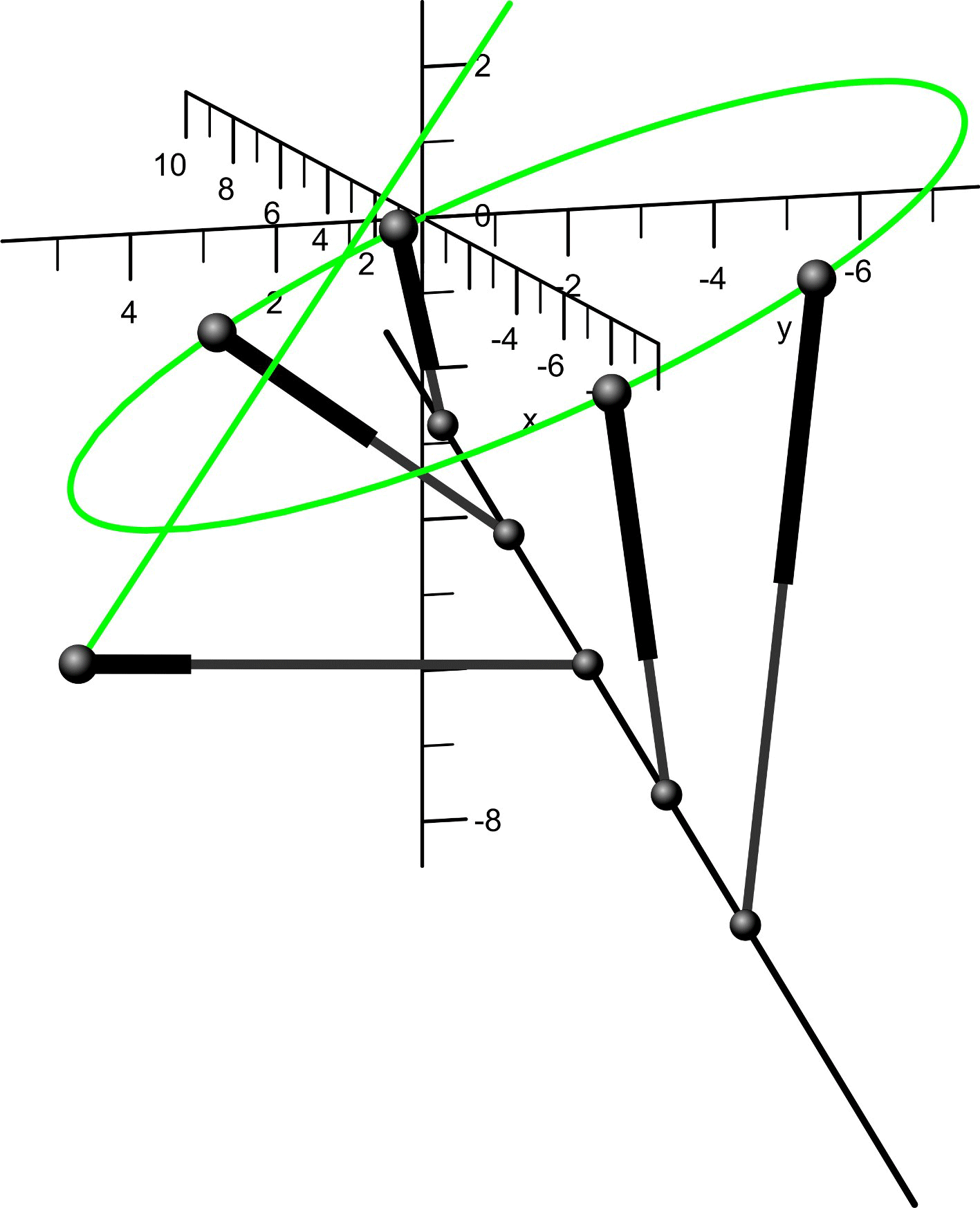
Finding all the transformations that leave the solution of a problem invariant does not solve it, but it provides a lot of information that contribute to its resolution. In the Stewart-Gough platform context, this indirect approach consists in the characterization of all the leg rearrangements that leave the platform singularity locus invariant. Such singularity-invariant leg rearrangements are shown to be a powerful tool to obtain kinematically equivalent manipulators, to help to visualize at a glance the complexity of its kinematics and to provide a common and original framework for the study of both pose-dependent singularities and architectural singularities of Stewart-Gough platforms.
The thesis analyzes all the rigid components that a Stewart-Gough platform can contain on a case-by-case basis. Then, it is shown how some of the most simple components admit any leg rearrangement that preserves the lines and planes that their attachments define. On the contrary, other more complex components only admit rearrangements that preserve some extra geometric constrains. This apparently restrictive fact will provide interesting geometric information about the kinematics and the topology of the singularity locus of the analyzed platforms.
In sum, this dissertation presents a new way to arrive at the geometric interpretations of Stewart-Gough platform singularities, a classification of these platforms depending on their singularities, and an inherent classification of all the architectural singularities, as well as some practical applications of these theoretical results.
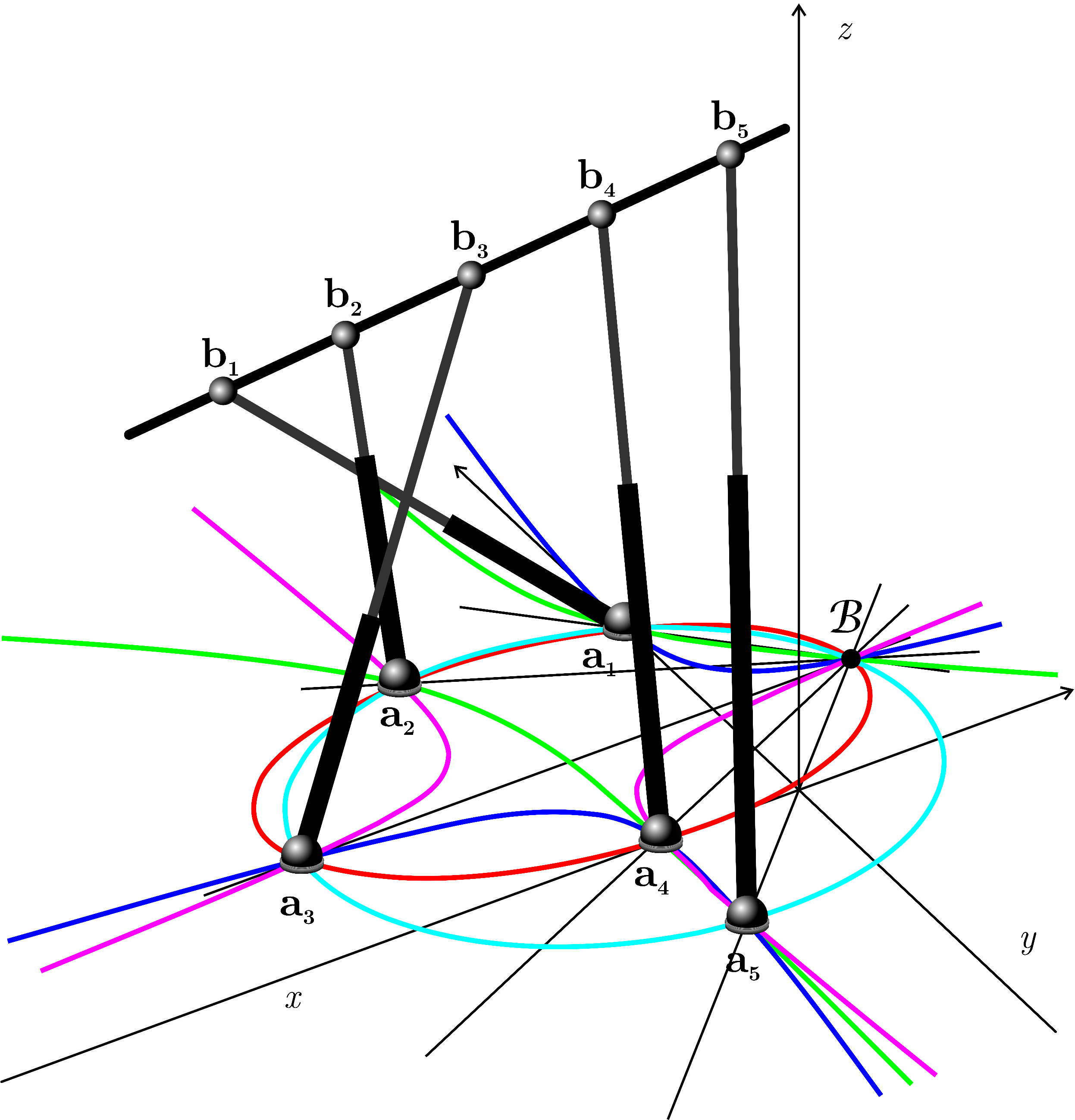
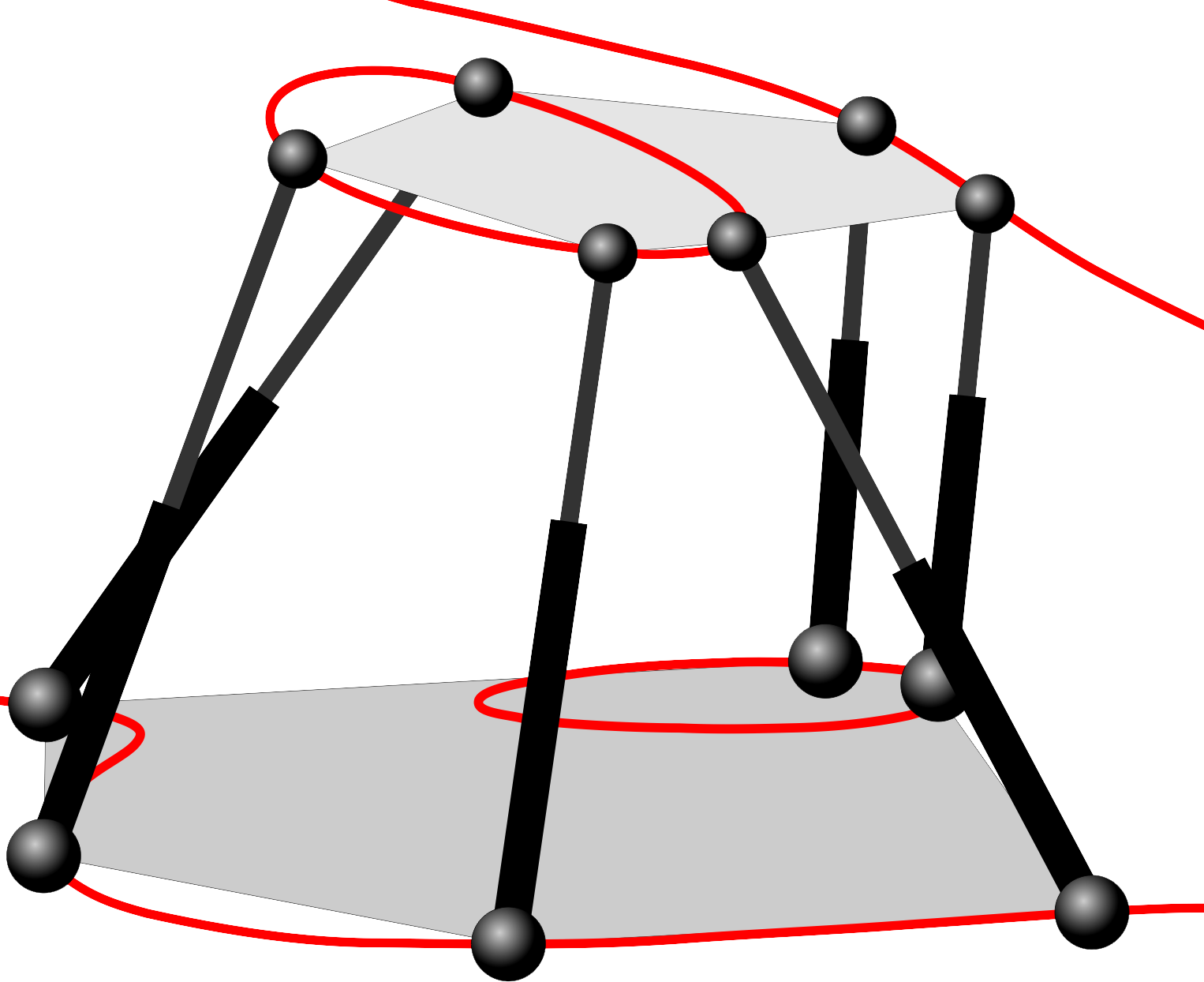
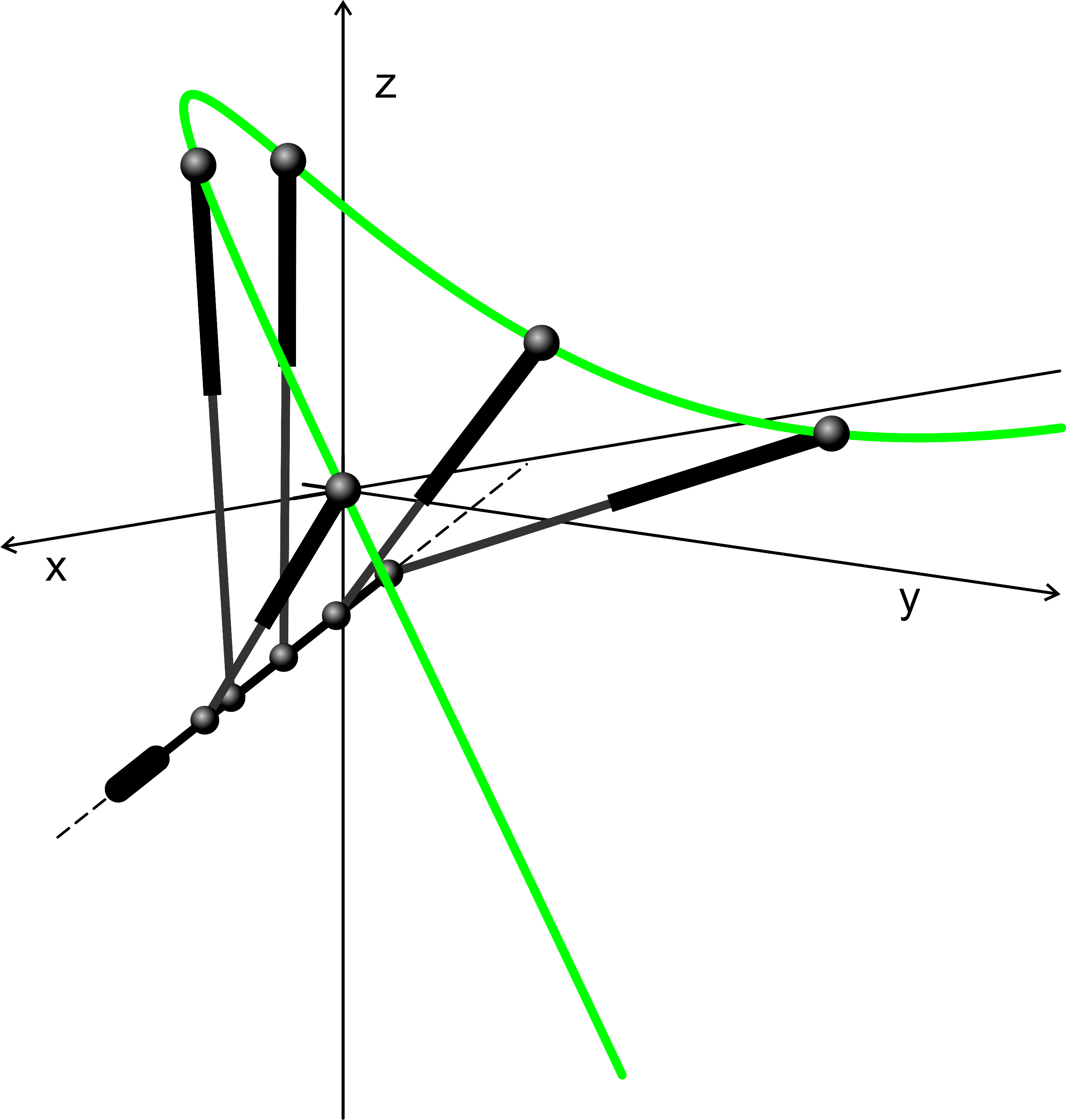
Some of the singularity-invariant leg rearrangements we have characterized:
The present thesis provides new insight into this problem from a completely new approach: finding singularity-invariant leg rearrangements.
Finding all the transformations that leave the solution of a problem invariant does not solve it, but it provides a lot of information that contribute to its resolution. In the Stewart-Gough platform context, this indirect approach consists in the characterization of all the leg rearrangements that leave the platform singularity locus invariant. Such singularity-invariant leg rearrangements are shown to be a powerful tool to obtain kinematically equivalent manipulators, to help to visualize at a glance the complexity of its kinematics and to provide a common and original framework for the study of both pose-dependent singularities and architectural singularities of Stewart-Gough platforms.
The thesis analyzes all the rigid components that a Stewart-Gough platform can contain on a case-by-case basis. Then, it is shown how some of the most simple components admit any leg rearrangement that preserves the lines and planes that their attachments define. On the contrary, other more complex components only admit rearrangements that preserve some extra geometric constrains. This apparently restrictive fact will provide interesting geometric information about the kinematics and the topology of the singularity locus of the analyzed platforms.
In sum, this dissertation presents a new way to arrive at the geometric interpretations of Stewart-Gough platform singularities, a classification of these platforms depending on their singularities, and an inherent classification of all the architectural singularities, as well as some practical applications of these theoretical results.



Some of the singularity-invariant leg rearrangements we have characterized: