Aims
Many situations in Robotics require the analysis of the motions of a complex closed-chain multibody system. Despite appearing very often in practice, there is a lack of general tools to effectively analyze and represent the configuration spaces of these sytems. This project aims at developing such tools. In all the situations to address, the valid configurations are implicitly defined by a system of loop-closure equations, encoding the various joint-assembly, task, or contact constraints intervening in the problem. Departing from this point, we address the following problems:
Position Analysis

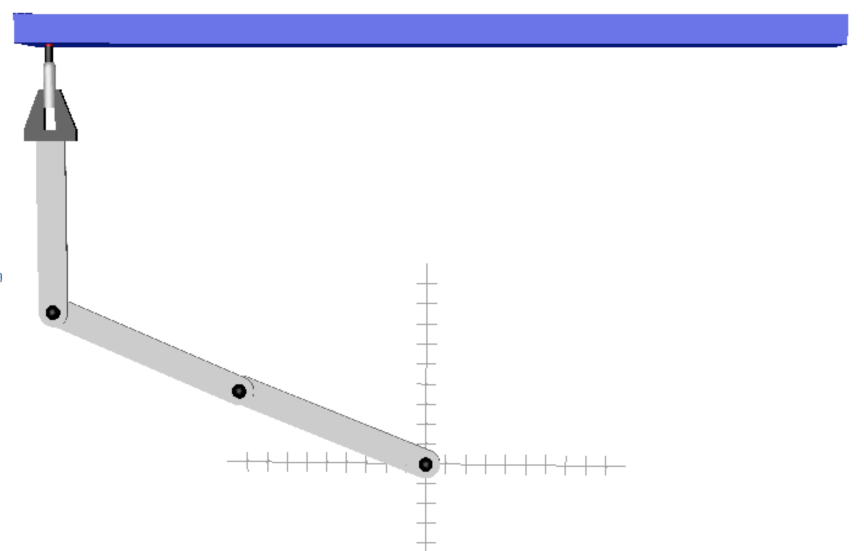
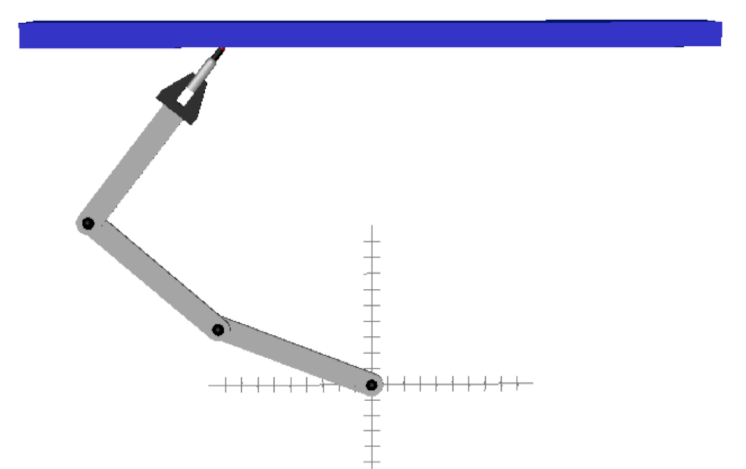
Welding on a fixed point with a fixed orientation. |
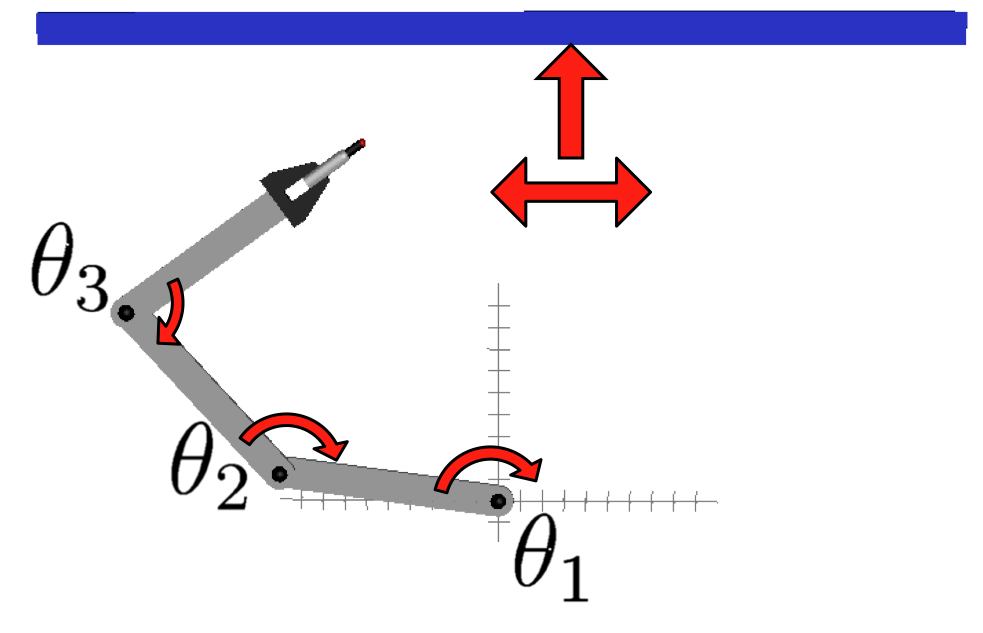
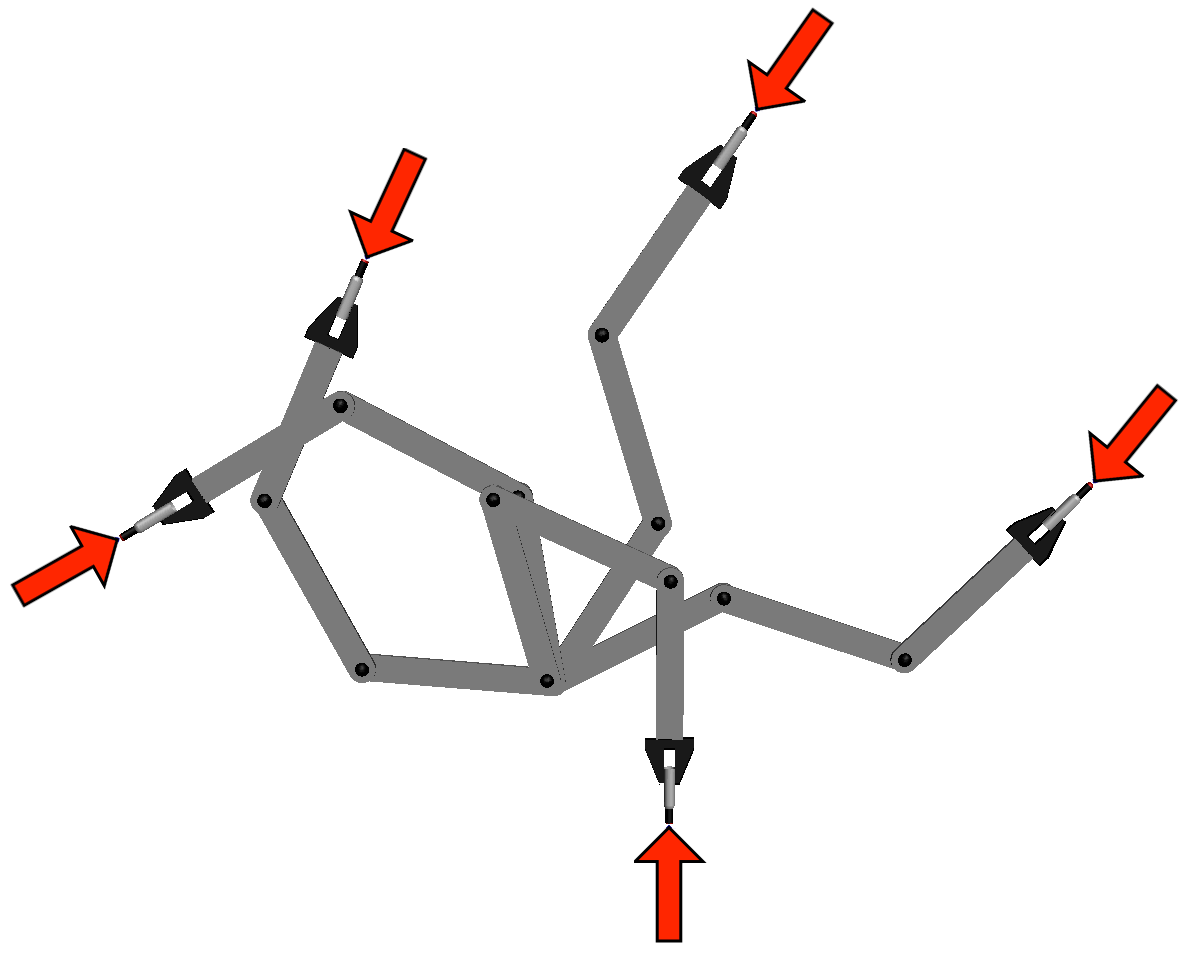
In an extreme case, the valid configurations are isolated points. This is what happens when solving position analysis problems on parallel or serial manipulators for example, where one wishes to find all the feasible configurations for given values of the input or output coordinates, the so-called forward and inverse kinematics problems. In this project, we proposed general tools to address these problems. A simple example can illustrate how the Cuik methods address this case. Consider the planar manipulator in the left figure. In this case two solutions exists, that are shown in the right figures (click on the images to enlarge them). The developed tools have proved to be successful on solving not only toy problems, but also the inverse/direct kinematics of general 6R robots and Stewart platforms. |

The two configurations solving the 0D welding task. 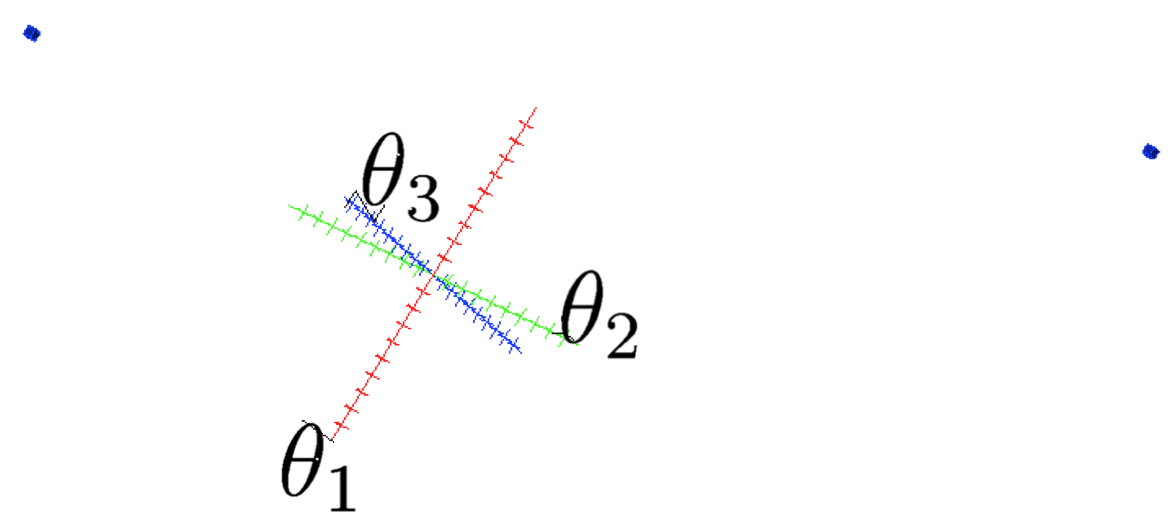
The configuration space solving the 0D welding task. |
Welding along a line with a fixed orientation. |
While typical inverse kinematic solvers can only identify the solutions when they are isolated points, our techniques can efficiently approximate positive-dimensional solution sets, and hence they can also be applied to solve problems where continua of solutions exist. For instance, if the welding robot has to weld not on a single point but on a line along the lower part of the beam, but keeping the tool orientation fixed, the resulting problem exhibits the one-dimensional manifold of solutions shown at the right. Using this technique, we can efficiently isolate complex configuration spaces that can not be isolated with any other existing technique. |
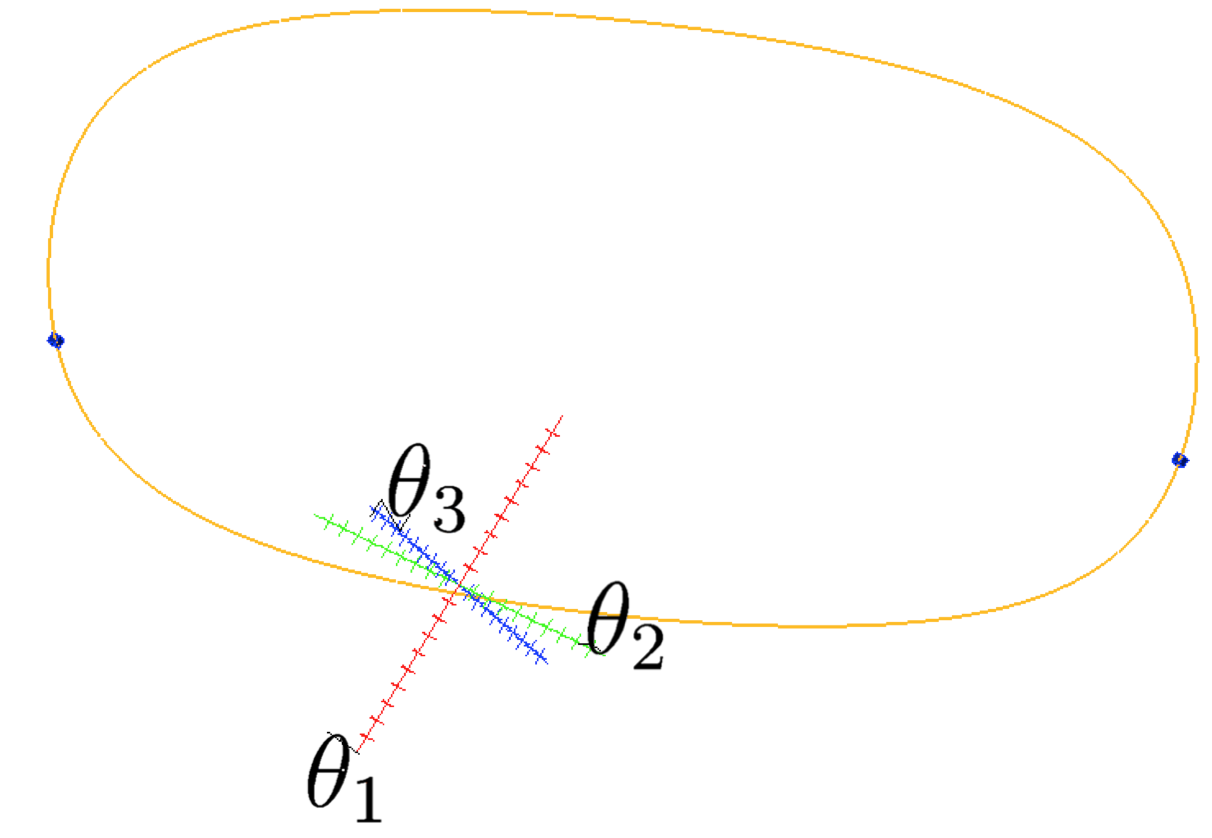
The configuration space solving the 1D welding task. |
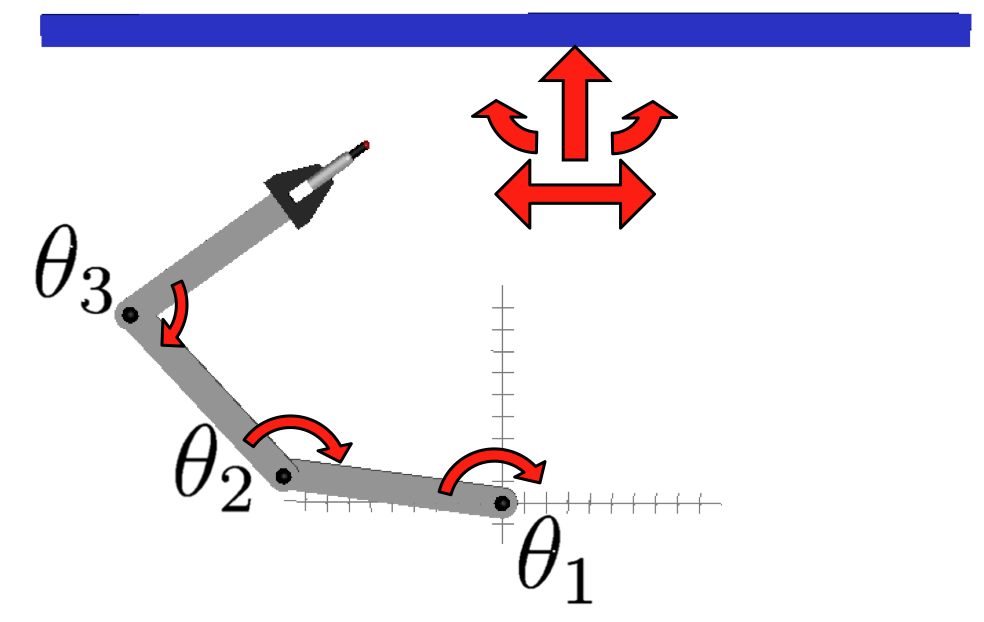
Welding along a line with a variable orientation. |
If the welding task is further relaxed and the tool can contact the beam with any orientation, the problem exhibits a two-dimensional C-space. To solve such difficult problems in reasonable time, we implemented a parallel version of the solver which can be executed in computer grids of arbitrary size. For instance, we executed it in our solver in our in-house grid and in the Marenostrum supercomputer, available at the Barcelona Supercomputer Center. In this way, we managed to isolate the full conformational space of the cylooctane for the first time. |
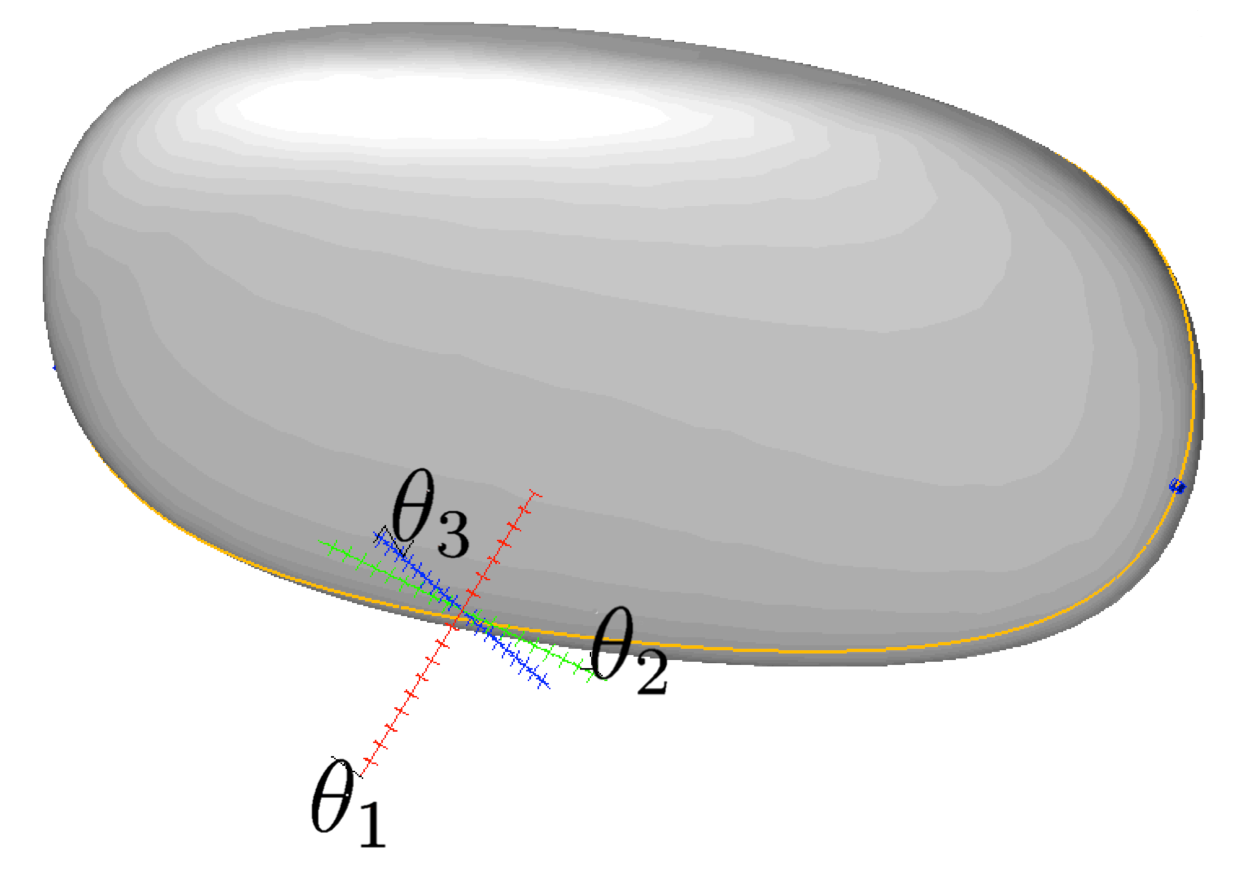
The configuration space solving the 2D welding task. |
Some configurations can lead to control or dexterities loses. |
As the dimensionality of the C-space increases, they become richer and possibly include lower dimensional subsets, such as the singularities or the workspace boundaries, which deserve a particular analysis. In the singularity loci, problematic losses of control or dexterity arise. The workspace boundaries provide the operational limits for the analyzed robot. Thus, the ability to compute these sets is essential not only to anticipate possible problems during robot operation, but also to provide valuable information to the robot designer. We developed tools to isolate all singular configurations and the workspace boundaries of a manipulator by appropriately formulating their equations and passing them to our solver, becoming the first general tool able to do so, up to the our knowledge. For example, the welding robot shown to the left, might exibit a one-dimensional loci of singularities such as that shown at the left, which corresponds to the configurations where two links are aligned. This technique can be used to identify complex singularity loci and workspace boundaries such as the ones of a 3RR planar manipulator. |

The singularity set of the welding task (in red). |

The path planning problem entails to find a safe path between two given configurations. |
We develop strategies to connect start and goal configurations through low-cost, collision- or singularity-free paths. Moreover, we develop randomized versions of such tools to deal with larger-dimensional spaces, based on the contruction of rapidly-exploring random trees through the manifold C-space. However, paths generated with RRT-like algorithms are typically jerky, which makes them unnecessarily long. To address this issue, we developed procedures to generate near-optimal paths when there is a cost function associated to the C-space. For instance, the two configurations shown at the right can be connected with the collision- and singularity-free path shown at the right. Using this technique it is possible to solve complex problems such as the singularity-free path planning of planar manipulators or path planning of dual-arm manipulations with service robots. |
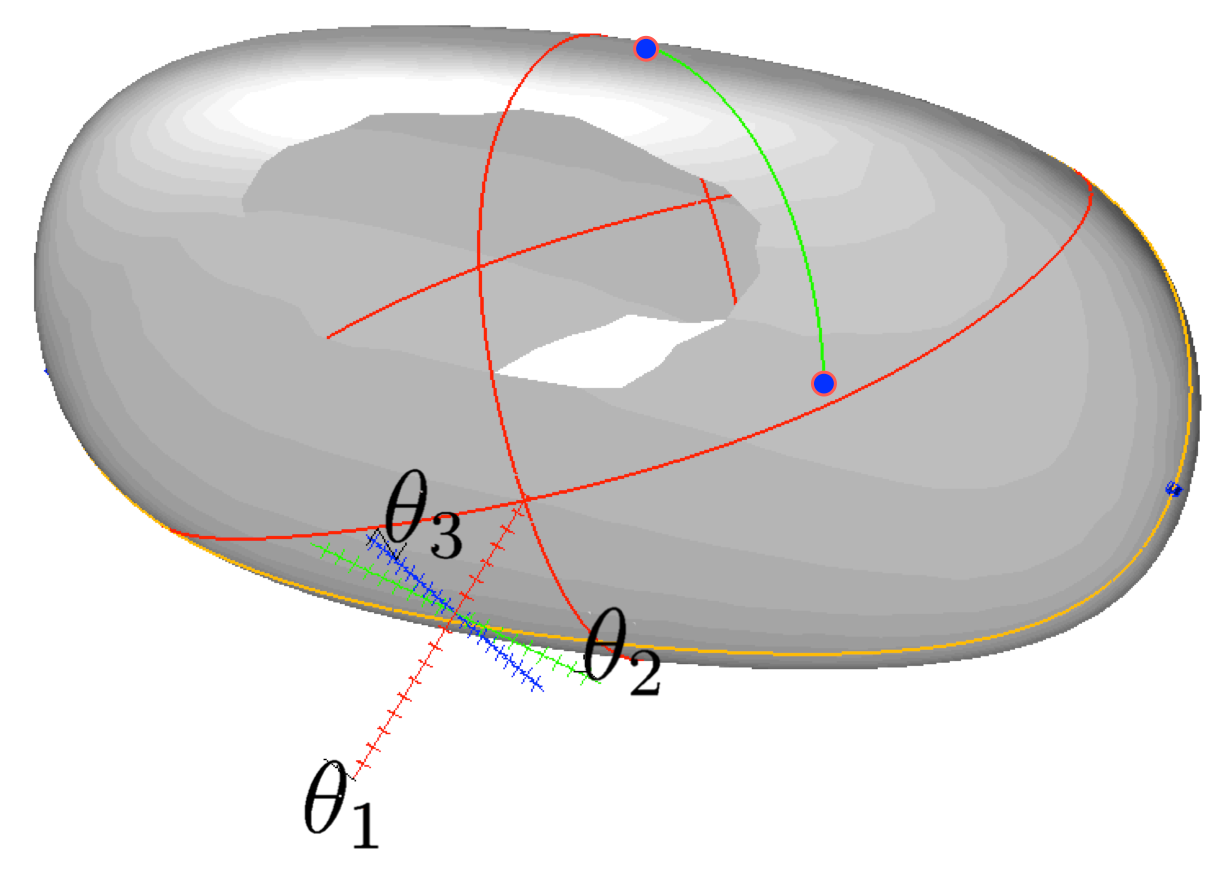
The path solving the path planning problem. |




Follow us!