Definition of basic functions (basically geomtric functions but also some other mathematical functions).
- Todo:
- Separate non-geometric functions fom the purely geometric ones.
- See Also
- geom.c.
Definition in file geom.h.
|
| boolean | pointLeftOfLine (double px, double py, double x1, double y1, double x2, double y2) |
| | Determines if a point is at the left of a vector. More...
|
| |
| boolean | pointRightOfLine (double px, double py, double x1, double y1, double x2, double y2) |
| | Determines if a point is at the right of a vector. More...
|
| |
| void | ComputeBoundingBox (unsigned int n, double *x, double *y, Tinterval *ix, Tinterval *iy) |
| | Determines the axis aligned bounding box of a set of points in R^2. More...
|
| |
| void | ComputeBoundingBox3d (unsigned int n, double *x, double *y, double *z, Tinterval *ix, Tinterval *iy, Tinterval *iz) |
| | Determines the axis aligned bounding box of a set of points in R^3. More...
|
| |
| void | SegmentCircleIntersection (double r2, double *x, double *y, double tol, unsigned int *n, double *xi, double *yi) |
| | Intersects a segment and a circle. More...
|
| |
| void | SegmentSphereIntersection (double r2, double *x, double *y, double *z, double tol, unsigned int *n, double *xi, double *yi, double *zi) |
| | Intersects a segment and a sphere. More...
|
| |
| void | Line2Points (double *x, double *y, boolean normalized, double *c) |
| | Defines a line given two points. More...
|
| |
| void | Plane3Points (double *x, double *y, double *z, boolean normalized, double *c) |
| | Defines a plane given 3 points. More...
|
| |
| boolean | RectangleCircleClipping (double r2, Tinterval *x, Tinterval *y, Tinterval *x_new, Tinterval *y_new) |
| | Clips a rectangle and a circle. More...
|
| |
| boolean | BoxSphereClipping (double r2, Tinterval *x, Tinterval *y, Tinterval *z, Tinterval *x_new, Tinterval *y_new, Tinterval *z_new) |
| | Clips a 3D box and a sphere. More...
|
| |
| boolean | RectangleParabolaClipping (Tinterval *x, double alpha, double beta, Tinterval *y, Tinterval *x_new, Tinterval *y_new) |
| | Clips a 2D box and a scaled parabola. More...
|
| |
| boolean | BoxSaddleClipping (Tinterval *x, Tinterval *y, double alpha, double beta, Tinterval *z, Tinterval *x_new, Tinterval *y_new, Tinterval *z_new) |
| | Clips a 3D box and a scaled saddle. More...
|
| |
| void | DefineNormalVector (double *v, double *n) |
| | Defines a unitary vector normal to a given vector. More...
|
| |
| void | CrossProduct (double *v1, double *v2, double *v3) |
| | Computes the cross product of two 3d vectors. More...
|
| |
| double | DotProduct (double *v1, double *v2) |
| | Computes the dot product of two 3d vectors. More...
|
| |
| boolean | NeighbouringTriangles (unsigned int *v1, unsigned int *v2) |
| | Determines if two sets of vertices define a neighbouring triangle. More...
|
| |
| boolean | SameTriangle (unsigned int *v1, unsigned int *v2) |
| | Identifies triangles formed by the same set of vertices. More...
|
| |
| double | Det2x2 (double *c1, double *c2) |
| | Determinant of a 2x2 matrix. More...
|
| |
| double | Det3x3 (double *c1, double *c2, double *c3) |
| | Determinant of a 3x3 matrix. More...
|
| |
| double | BallVolume (unsigned int n, double r) |
| | Volume of of a n-ball. More...
|
| |
| void | FirstCombination (unsigned int n, unsigned int m, unsigned int *cb) |
| | Initializes a combination. More...
|
| |
| boolean | NextCombination (unsigned int n, unsigned int m, unsigned int *cb) |
| | Moves to the next combination. More...
|
| |
| void | PrintReal (FILE *f, double r) |
| | Pretty print a real number. More...
|
| |
| void | Print3Reals (FILE *f, double r1, double r2, double r3) |
| | Pretty print three real number. More...
|
| |
| void | PrintAngle (FILE *f, double r) |
| | Pretty print an angle. More...
|
| |
| boolean pointLeftOfLine |
( |
double |
px, |
|
|
double |
py, |
|
|
double |
x1, |
|
|
double |
y1, |
|
|
double |
x2, |
|
|
double |
y2 |
|
) |
| |
Determines if a 2D point is at the left of a vector in R^2.
- Parameters
-
| px | X coordinate of the point. |
| py | Y coordinate of the point. |
| x1 | X coordinate of the first point defining the vector. |
| y1 | Y coordinate of the first point defining the vector. |
| x2 | X coordinate of the second point defining the vector. |
| y2 | Y coordinate of the second point defining the vector. |
- Returns
- TRUE if point at the left of the vector.
- See Also
- pointRightOfLine
Definition at line 18 of file geom.c.
References ROUNDDOWN, and ROUNDNEAR.
| boolean pointRightOfLine |
( |
double |
px, |
|
|
double |
py, |
|
|
double |
x1, |
|
|
double |
y1, |
|
|
double |
x2, |
|
|
double |
y2 |
|
) |
| |
Determines if a 2D point is at the right of a vector in R^2.
- Parameters
-
| px | X coordinate of the point. |
| py | Y coordinate of the point. |
| x1 | X coordinate of the first point defining the vector. |
| y1 | Y coordinate of the first point defining the vector. |
| x2 | X coordinate of the second point defining the vector. |
| y2 | Y coordinate of the second point defining the vector. |
- Returns
- TRUE if point at the right of the vector.
- See Also
- pointLeftOfLine
Definition at line 34 of file geom.c.
References ROUNDNEAR, and ROUNDUP.
| void ComputeBoundingBox |
( |
unsigned int |
n, |
|
|
double * |
x, |
|
|
double * |
y, |
|
|
Tinterval * |
ix, |
|
|
Tinterval * |
iy |
|
) |
| |
Determines the axis aligned bounding box of a set of points in R^2.
- Parameters
-
| n | The number of points to be bounded. |
| x | Array with the X coordinates of the points. |
| y | Array with the Y coordinates of the points. |
| ix | Output interval in the X axis. |
| iy | Output interval in the Y axis. |
Definition at line 53 of file geom.c.
References NewInterval().
Determines the axis aligned bounding box of a set of points in R^3.
- Parameters
-
| n | The number of points to be bounded. |
| x | Array with the X coordinates of the points. |
| y | Array with the Y coordinates of the points. |
| z | Array with the Z coordinates of the points. |
| ix | Output interval in the X axis. |
| iy | Output interval in the Y axis. |
| iz | Output interval in the Z axis. |
Definition at line 73 of file geom.c.
References NewInterval().
| void SegmentCircleIntersection |
( |
double |
r2, |
|
|
double * |
x, |
|
|
double * |
y, |
|
|
double |
tol, |
|
|
unsigned int * |
n, |
|
|
double * |
xi, |
|
|
double * |
yi |
|
) |
| |
Intersects the circle
![\[x^2+y^2=r^2\]](form_25.png)
with the segment defined by two 2d points given in vectors x and y.
The output includes at most two points (stored in xi and yi whose space must be allocated by the caller)
The implementation is numerically save in the sense that it returns as many solutions are possible. However the returned solution can be slightly out of the segment due to numerical issues (the only way to avoid this is to return an interva instead of a point).
- Parameters
-
| r2 | Squared radious of the circle. |
| x | X component of the two points defining the segment. |
| y | Y component of the two points defining the segment. |
| tol | Numerical tolerance. Used to accept as a solutions points not extrictly on the segment but very close to its extremes. |
| n | Number of intersections. This can be 0, 1 or 2. |
| xi | X component of the n intersection points detected. |
| yi | Y component of the n intersection points detected. |
Definition at line 98 of file geom.c.
References EmptyInterval(), Error(), INF, Intersection(), IntervalAdd(), IntervalCenter(), IntervalDivision(), IntervalInvert(), IntervalOffset(), IntervalPow(), IntervalProduct(), IntervalScale(), IntervalSqrt(), IntervalSubstract(), IsInside(), and NewInterval().
| void SegmentSphereIntersection |
( |
double |
r2, |
|
|
double * |
x, |
|
|
double * |
y, |
|
|
double * |
z, |
|
|
double |
tol, |
|
|
unsigned int * |
n, |
|
|
double * |
xi, |
|
|
double * |
yi, |
|
|
double * |
zi |
|
) |
| |
Intersects the circle
![\[x^2+y^2+z^2=r^2\]](form_26.png)
with the segment defined by two 3d points given in vectors x, y, and z.
The output includes at most two points (stored in xi, yi, and zi whose space must be allocated by the caller)
The implementation is numerically save in the sense that it returns as many solutions are possible. However the returned solution can be slightly out of the segment due to numerical issues (the only way to avoid this is to return an interva instead of a point).
- Parameters
-
| r2 | Squared radious of the circle. |
| x | X component of the two points defining the segment. |
| y | Y component of the two points defining the segment. |
| z | Z component of the two points defining the segment. |
| tol | Numerical tolerance. Used to accept as a solutions points not extrictly on the segment but very close to its extremes. |
| n | Number of intersections. This can be 0, 1 or 2. |
| xi | X component of the n intersection points detected. |
| yi | Y component of the n intersection points detected. |
| zi | Z component of the n intersection points detected. |
Definition at line 185 of file geom.c.
References EmptyInterval(), Error(), INF, Intersection(), IntervalAdd(), IntervalCenter(), IntervalDivision(), IntervalInvert(), IntervalOffset(), IntervalPow(), IntervalProduct(), IntervalScale(), IntervalSqrt(), IntervalSubstract(), IsInside(), and NewInterval().
| void Line2Points |
( |
double * |
x, |
|
|
double * |
y, |
|
|
boolean |
normalized, |
|
|
double * |
c |
|
) |
| |
Defines the parameters of a 2d line given two points.
- Parameters
-
| x | The X component of the two points. |
| y | The Y component of the two points. |
| normalized | TRUE if the output line parameters should be normalized. |
| c | The coeficients of the output line (3 values, space allocated by the caller). |
Definition at line 289 of file geom.c.
References Error(), and ZERO.
| void Plane3Points |
( |
double * |
x, |
|
|
double * |
y, |
|
|
double * |
z, |
|
|
boolean |
normalized, |
|
|
double * |
c |
|
) |
| |
Defines the parameters of a 3d plane given 3 points.
- Parameters
-
| x | The X component of the three points. |
| y | The Y component of the three points. |
| z | The Z component of the three points. |
| normalized | TRUE if the output plane parameters should be normalized. |
| c | The coeficients of the output plane (4 values, space allocated by the caller). |
Definition at line 313 of file geom.c.
References CrossProduct(), Error(), and ZERO.
Reduces the ranges defining a 3D box so that it is adjusted to a zero centered sphere with a given radius.
- Parameters
-
| r2 | Squared radius of the sphere. |
| x | Interval defining the X axis for the 3D box. |
| y | Interval defining the Y axis for the 3D box. |
| z | Interval defining the Z axis for the 3D box. |
| x_new | Interval defining the X axis of the box after the clipping. |
| y_new | Interval defining the Y axis of the box after the clipping. |
| z_new | Interval defining the Z axis of the box after the clipping. |
- Returns
- TRUE if the intersection is not empty.
Definition at line 401 of file geom.c.
References Intersection(), IntervalAdd(), IntervalInvert(), IntervalPow(), IntervalSqrt(), NewInterval(), ROUNDNEAR, ROUNDUP, Union(), and ZERO.
Referenced by CropEquation().
Reduces the ranges defining a 2D box so that it is adjusted to a offest, scaled parabola, 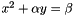 . .
- Parameters
-
| x | Interval defining the X axis for the 2D box. |
| alpha | The scale factor. |
| beta | The offset factor. |
| y | Interval defining the Y axis for the 2D box. |
| x_new | Interval defining the X axis of the box after the clipping. |
| y_new | Interval defining the Y axis of the box after the clipping. |
- Returns
- TRUE if the intersection is not empty.
Definition at line 473 of file geom.c.
References Intersection(), IntervalInvert(), IntervalOffset(), IntervalPow(), IntervalProduct(), IntervalScale(), IntervalSqrt(), NewInterval(), ROUNDDOWN, ROUNDNEAR, ROUNDUP, and Union().
Referenced by CropEquation().
Reduces the ranges defining a 3D box so that it is adjusted to offest, scaled saddle equation, 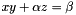 . .
- Parameters
-
| x | Interval defining the X axis for the 3D box. |
| y | Interval defining the Y axis for the 3D box. |
| alpha | The scale factor. |
| beta | The offset factor. |
| z | Interval defining the Z axis for the 3D box. |
| x_new | Interval defining the X axis of the box after the clipping. |
| y_new | Interval defining the Y axis of the box after the clipping. |
| z_new | Interval defining the Z axis of the box after the clipping. |
- Returns
- TRUE if the intersection is not empty.
Definition at line 518 of file geom.c.
References CopyInterval(), Intersection(), IntervalDivision(), IntervalInvert(), IntervalOffset(), IntervalProduct(), IntervalScale(), IsInside(), NewInterval(), ROUNDDOWN, ROUNDNEAR, and ROUNDUP.
Referenced by CropEquation().
| void DefineNormalVector |
( |
double * |
v, |
|
|
double * |
n |
|
) |
| |
Defines a unitary vector normal to a given vector in R^3. Observe that there is a continous set of normal vectors to a given vector. We just pick one of them.
- Parameters
-
| v | The output vector. |
| n | The reference vector. |
Definition at line 571 of file geom.c.
References Error().
Referenced by main(), NewRevoluteJoint(), and NewUniversalJoint().
| void CrossProduct |
( |
double * |
v1, |
|
|
double * |
v2, |
|
|
double * |
v3 |
|
) |
| |
Computes the cross product of two 3d vectors.
- Parameters
-
| v1 | First 3d vector. |
| v2 | Second 3d vector. |
| v3 | The output 3d vector. |
Definition at line 630 of file geom.c.
Referenced by Atoms2Transforms(), EvaluatePATrans(), EvaluateTransSeq(), GetJointDOFValues(), GetJointTransform(), InitPatchTrans(), NewInPatchJoint(), NewRevoluteJoint(), NewUniversalJoint(), Plane3Points(), and TriangulateAtlas().
| double DotProduct |
( |
double * |
v1, |
|
|
double * |
v2 |
|
) |
| |
| boolean NeighbouringTriangles |
( |
unsigned int * |
v1, |
|
|
unsigned int * |
v2 |
|
) |
| |
Determines if two triangles are neighbours. Checks if the two triangles share two vertices.
Whe assume the vertices in each triangle to be different.
- Parameters
-
| v1 | The index of the three vertices defining the first triangle. |
| v2 | The index of the three vertices defining the second triangle. |
- Returns
- TRUE if the two triangles share two vertices.
Definition at line 648 of file geom.c.
Referenced by TriangulateAtlas().
| boolean SameTriangle |
( |
unsigned int * |
v1, |
|
|
unsigned int * |
v2 |
|
) |
| |
Determines if two triangles are defined over the same set of vertices.
Whe assume the vertices in each triangle to be different.
- Parameters
-
| v1 | The index of the three vertices defining the first triangle. |
| v2 | The index of the three vertices defining the second triangle. |
- Returns
- TRUE if the two triangles share the three vertices.
Definition at line 662 of file geom.c.
References TRUE.
Referenced by TriangulateAtlas().
| double Det2x2 |
( |
double * |
c1, |
|
|
double * |
c2 |
|
) |
| |
Determinant of a 2x2 matrix given by columns. This is used to solve small lineal systems.
- Parameters
-
| c1 | The first column. |
| c2 | The first column. |
- Returns
- The determinant.
Definition at line 725 of file geom.c.
Referenced by GetJointDOFValues().
| double Det3x3 |
( |
double * |
c1, |
|
|
double * |
c2, |
|
|
double * |
c3 |
|
) |
| |
Determinant of a 3x3 matrix given by columns. This is used to solve small lineal systems.
- Parameters
-
| c1 | The first column. |
| c2 | The first column. |
| c3 | The first column. |
- Returns
- The determinant.
Definition at line 730 of file geom.c.
Referenced by GetJointDOFValues().
| double BallVolume |
( |
unsigned int |
n, |
|
|
double |
r |
|
) |
| |
| void FirstCombination |
( |
unsigned int |
n, |
|
|
unsigned int |
m, |
|
|
unsigned int * |
cb |
|
) |
| |
Initializes a combination of n numbers with 0 to m (included) options per number.
- Parameters
-
| n | The number of entries in the combiation. |
| m | The number of options for each entry. |
| cb | Array where to store the combination. |
Definition at line 697 of file geom.c.
Referenced by DefinePolytope().
| boolean NextCombination |
( |
unsigned int |
n, |
|
|
unsigned int |
m, |
|
|
unsigned int * |
cb |
|
) |
| |
Iterates to the next combination of n numbers with up to m values per number.
- Parameters
-
| n | The number of entries in the combiation. |
| m | The number of options for each entry. |
| cb | Array where to store the combination. |
- Returns
- TRUE if the next combination actually exits.
Definition at line 705 of file geom.c.
References FALSE, and TRUE.
Referenced by DefinePolytope().
| void PrintReal |
( |
FILE * |
f, |
|
|
double |
r |
|
) |
| |
| void Print3Reals |
( |
FILE * |
f, |
|
|
double |
r1, |
|
|
double |
r2, |
|
|
double |
r3 |
|
) |
| |
Prints three real numbers separated by commas.
- Parameters
-
| f | The file where to print the number. |
| r1 | The first number to print. |
| r2 | The second number to print. |
| r3 | The third number to print. |
Definition at line 754 of file geom.c.
References PrintReal().
Referenced by PrintPolyhedron().
| void PrintAngle |
( |
FILE * |
f, |
|
|
double |
r |
|
) |
| |
Prints an angle rounding to 0,pi,-pi,pi/2,-pi/2, if it is the case.
- Parameters
-
| f | The file where to print the number. |
| r | The angle to print. |
Definition at line 764 of file geom.c.
References M_PI, and ZERO.
|
![\[x^2+y^2=r^2\]](form_25.png)
![\[x^2+y^2+z^2=r^2\]](form_26.png)
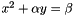 .
.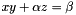 .
.
Follow us!