Trisector Directory Reference

Detailed Description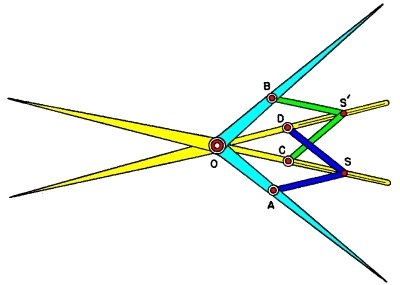

[Introduction] [Geometry] [Process] [Statistics] [Results] [References]

Introduction

Angle trisection is the division of an arbitrary angle into three equal angles. It was one of the three geometric problems of antiquity for which solutions using only compass and straightedge were sought. The problem was algebraically proved impossible by Wantzel in 1836.

A variety of mechanisms have been devised for the solution of the trisection problem. Some of these mechanisms draw the curves that aid in the solution of the Trisection equation; others solve the equation directly, or are applicable to the immediate division of the angle into three equal parts. An example of the latter sort is "Laisant's Compass", shown in the figure above. It was proposed by M. Laisant in 1875 [Brocard 1875], and is composed of four straight bars hinged together at one point and forced to make equal angles with each other. See [Yates 1941] for an interesting review of the trisection problem.

The benchmark is chosen to illustrate cuik's performance on problems that are unsolvable by ruler-and-compass solvers. While it is true this linkage can be simulated with dynamic geometry software like Cinderella or Sketchpad, the resulting construction can only solve the reverse problem, angle triplication, and cannot sistematically trace all branches of the linkage motion.

Geometry

The lengths are chosen so that OB = OC, CS' = BS', OD = OA, and AS = DS, with S and S' as joints permitted to slide in straight grooves along the two trisecting bars. The triangles OBS', ODS' and OAS are congruent with equal angles at O. The bars OS' and OS are extended beyond O so that the third part can be set off upon the same arc.

The particular trisector we use has the folowing sizes:

• OA = OB = OC = OD = AS = DS = BS' = CS' = 2.3

Process

The instructions on how to process the examples are given in each separate file:

• Trisector_fixed.world Gives a formulation where the input angle is fixed. With this the solution space of the linkage becomes 0-dimensional.
• Trisector.world Is a formulation that yields a 1-dof solution set since the input angle is let free.

Statistics

Characteristics of the problem:

	Fixed	Mobile
Nr. of indep. loops	4	4
Nr. of links	10	10
Nr. of joints	9	9
Nr. of equations (in the simplified system)	14	15
Nr. of variables (in the simplified system)	14	16

Here you have the statistics about the execution (on an Intel Core i7 at 2.9 Ghz).

	Fixed	Mobile
Nr. of Empty boxes	0	4
Nr. of Solution boxes	1	353
Execution time (s)	0.2	27

Results

This is the valid configuration for the problem with the input angle fixed: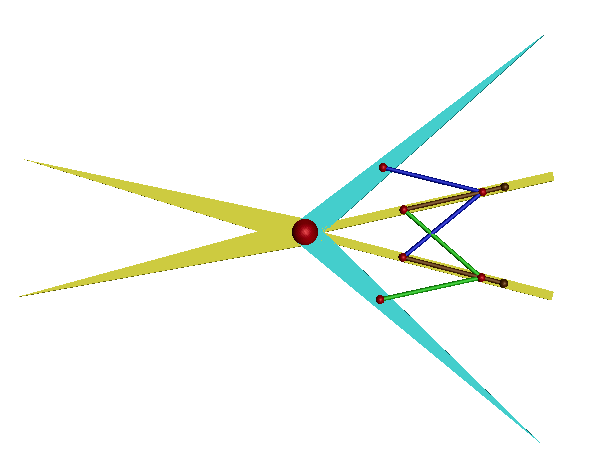

This is the configuration space for the problem when the input angle is free

And here you have an animation of part of this configuration space.

References

• R.C. Yates, "The Trisection Problem", National Mathematics Magazine, Vol. 15, No. 6, pp. 278-293, 1941.
• H. Brocard, , "Note sur un compas trisecteur proposé par M. Laisant", Bulletin de la S.M.F., tome 3, p. 47-48, 1875.

Files
file	Trisector.world [code]
	Mobile Laisant angle trisector.
file	Trisector_fixed.world [code]
	Fixed Laisant angle trisector.