Intranet|
atlas.c File Reference Detailed DescriptionImplementation of a set of local charts on a manifold. Definition in file atlas.c.
Function Documentation
Init the atlas built statistics.
Definition at line 688 of file atlas.c. References TAtlasStatistics::nBifurcations, TAtlasStatistics::nBoundaryAttempts, TAtlasStatistics::nExtensions, TAtlasStatistics::nFarFromParent, TAtlasStatistics::nGoodExtension, TAtlasStatistics::nImpossible, TAtlasStatistics::nInCollision, TAtlasStatistics::nLargeError, TAtlasStatistics::nNoJumpBranch, TAtlasStatistics::nNonRegularPoint, TAtlasStatistics::nNoSingularEnough, TAtlasStatistics::nNotInBoundary, TAtlasStatistics::nNotInManifold, TAtlasStatistics::nQRSVDError, TAtlasStatistics::nRadiousChange, TAtlasStatistics::nSingImpossible, TAtlasStatistics::nSmallAngle, and TAtlasStatistics::nSPMissed. Referenced by AtlasAStar(), AtlasGBF(), and BuildAtlasFromPoint().
New attempt to extend the atlas.
Definition at line 713 of file atlas.c. References TAtlasStatistics::nExtensions. Referenced by ExtendAtlasFromPoint(), and ExtendAtlasTowardPoint().
New attempt to generate a point on the boundary.
Definition at line 719 of file atlas.c. References TAtlasStatistics::nBoundaryAttempts. Referenced by AtlasAStar(), AtlasGBF(), and BuildAtlasFromPoint().
New time we failed to generate a point on the boundary.
Definition at line 725 of file atlas.c. References TAtlasStatistics::nNotInBoundary. Referenced by AtlasAStar(), AtlasGBF(), and BuildAtlasFromPoint().
New time the point in the tangent space was too far form the manifold.
Definition at line 731 of file atlas.c. References TAtlasStatistics::nLargeError. Referenced by ExtendAtlasFromPoint(), and ExtendAtlasTowardPoint().
The chart initialization failed since the given point is non-regular up to the given numerical error.
Definition at line 737 of file atlas.c. References TAtlasStatistics::nNonRegularPoint. Referenced by ExtendAtlasFromPoint(), and ExtendAtlasTowardPoint().
The chart initialization failed since the given point is not on the manifold.
Definition at line 743 of file atlas.c. References TAtlasStatistics::nNotInManifold. Referenced by ExtendAtlasFromPoint(), and ExtendAtlasTowardPoint().
The chart initialization failed since the QR or SVD decomposition used to compute the tangent space failed.
Definition at line 749 of file atlas.c. References TAtlasStatistics::nQRSVDError. Referenced by ExtendAtlasFromPoint(), and ExtendAtlasTowardPoint().
New time the point was too far from parent. The distance is measured not only in Euclidena space but we also compare the tangent spaces (they must be similar).
Definition at line 755 of file atlas.c. References TAtlasStatistics::nFarFromParent. Referenced by ExtendAtlasFromPoint(), and ExtendAtlasTowardPoint().
New time the point was too far in collision.
Definition at line 761 of file atlas.c. References TAtlasStatistics::nInCollision. Referenced by ExtendAtlasTowardPoint().
New time we had to change the sampling radious to get a new chart.
Definition at line 767 of file atlas.c. References TAtlasStatistics::nRadiousChange. Referenced by ExtendAtlasFromPoint(), and ExtendAtlasTowardPoint().
New time we actually succeeded in creating a new chart.
Definition at line 773 of file atlas.c. References TAtlasStatistics::nGoodExtension. Referenced by ExtendAtlasFromPoint(), and ExtendAtlasTowardPoint().
When extending from a point we progressively reduce the radious of expansion until we find a point where it its possible to properly define a new chart. In some wear situations even reducing the radius below the given MIN_SAMPLING_RADIUS, it is impossible to generate a child chart. Note that this should never happen but it actually occurs due to numerical issues. When extending towards a point, the situations arises when even at the first step of the motion toward the new point the generation of a new chart fails. In general this is a ill-posed situation and we should trigger an error and stop the chart construction. In some cases, however we just mark the problematic point and continue the atlas extension. Note that this can lead to incomplete atlas if the skiped point was actually necessary to complete the manifold coverage. If we tolerate this error, at least we count how many times this awful situation actually occurs. If it occurs few times we can assume that the chart is fully constructed (the skiped point is likely to be covered when expanding from/toward another point). If we have many situations of this type we have to assume we ended up with an incomplete atlas and to solve the issue. Many times using a smaller Epsilon. Definition at line 779 of file atlas.c. References TAtlasStatistics::nImpossible. Referenced by ExtendAtlasFromPoint(), and ExtendAtlasTowardPoint().
This is like the situation for NewImpossible but when it occurs on a singular chart. We have to tolerate this situations since the mapping from the chart to the manifold then to be ill-conditioned when close to the singularity and it may fail. For normal charts we have the hypothesis that this mapping is safer as closer to the chart center. Definition at line 785 of file atlas.c. References TAtlasStatistics::nSingImpossible. Referenced by ExtendAtlasFromPoint(), and ExtendAtlasTowardPoint().
A new bifurcation is processed.
Definition at line 791 of file atlas.c. References TAtlasStatistics::nBifurcations. Referenced by ProcessBifurcation().
We managed to detect the bifurcation, detect the singular point and jump but the tangent space at the new point is too similar to the one at the known branch of the variety. This problably means that the ended up in the same branch of the variety (it could also mean that the two branches intersect with a very small angle) Definition at line 797 of file atlas.c. References TAtlasStatistics::nSmallAngle. Referenced by DefineChartsAtBifurcation().
We detected a bifurcation but did not manage to locate the singular point.
Definition at line 803 of file atlas.c. References TAtlasStatistics::nSPMissed. Referenced by ProcessBifurcation().
We detected a bifurcation and located a singular point but the tangent space defined at the singular point is only of dimension 'k' (it should be of dimension k+1). Without the additional vector in the tangent space we can not jump to the new branch. Definition at line 809 of file atlas.c. References TAtlasStatistics::nNoSingularEnough. Referenced by ProcessBifurcation().
We detected the bifurcation, located the singular point, computed the additional vector of the tangent space at this point but we did not managed to actually jump to the other branch of the variety. Definition at line 815 of file atlas.c. References TAtlasStatistics::nNoJumpBranch. Referenced by ProcessBifurcation().
Definition at line 821 of file atlas.c. References CT_DETECT_BIFURCATIONS, GetParameter(), TAtlasStatistics::nBifurcations, TAtlasStatistics::nBoundaryAttempts, TAtlasStatistics::nExtensions, TAtlasStatistics::nFarFromParent, TAtlasStatistics::nGoodExtension, TAtlasStatistics::nImpossible, TAtlasStatistics::nInCollision, TAtlasStatistics::nLargeError, TAtlasStatistics::nNoJumpBranch, TAtlasStatistics::nNonRegularPoint, TAtlasStatistics::nNoSingularEnough, TAtlasStatistics::nNotInBoundary, TAtlasStatistics::nNotInManifold, TAtlasStatistics::nQRSVDError, TAtlasStatistics::nRadiousChange, TAtlasStatistics::nSingImpossible, TAtlasStatistics::nSmallAngle, and TAtlasStatistics::nSPMissed. Referenced by AtlasAStar(), AtlasGBF(), and BuildAtlasFromPoint().
Charts are added to the atlas and latter on they are post-processed. In this post-process we determine the neighbours for each chart and detect possible bifurcations. The post-process must be called after any atlas extension for a given chart (this can include the generation of one or more children charts).
Definition at line 893 of file atlas.c. References Tatlas::currentChart, DetermineChartNeighbours(), Tatlas::nBifurcations, NO_UINT, Tatlas::npBifurcations, Tatlas::npCharts, ProcessBifurcation(), and Warning(). Referenced by AddChart2Atlas(), AddTrustedChart2Atlas(), AtlasAStar(), BuildAtlasFromPoint(), DefineChartsAtBifurcation(), ExtendAtlasFromPoint(), and ExtendAtlasTowardPoint().
This is very similar to ExtendAtlasFromPoint but we do not take statistics of the atlas construction and the treatment of the atlas borders is simpler. Moreover, we do not add the chart to the atlas, but just generate a new chart (if no error is encountered in the process). Latter on we have to add the generated chart to the atlas (detecting neighbours and dealing with bifurcations, if any). This is used when parallelizing the atlas construction process: all the external vertexes of a chart can be processed in parallel and the resulting charts added to the atlas (search for neighbours and treat bifurcations) in sequence.
Definition at line 919 of file atlas.c. References Tatlas::ambient, Tatlas::ce, Chart2Manifold(), ChartIsFrontier(), Tatlas::charts, CloseCharts(), CollisionChart(), CS_WD_SIMP_INEQUALITIES_HOLD, CT_EPSILON, DeleteChart(), Tatlas::e, FALSE, GetParameter(), InitChart(), Tatlas::J, Tatlas::k, Tatlas::m, MIN_SAMPLING_RADIUS, NEW, Norm(), PointInBoxTopology(), Tatlas::r, SAMPLING_RADIUS_REDUCTION_FACTOR, ScaleVector(), Tatlas::simpleChart, Tatlas::tp, TRUE, and Tatlas::w. Referenced by AtlasAStar(), and BuildAtlasFromPoint().
Defines the path between the start and goal configurations navigating along the paths found in the atlas.
Definition at line 1463 of file atlas.c. References AddSample2Samples(), ATLAS_VERBOSE, Tatlas::charts, CS_WD_REGENERATE_ORIGINAL_POINT, GetChartCenter(), InitSamples(), Tatlas::J, Tatlas::k, Manifold2Chart(), NEW, NO_UINT, Norm(), PathInChart(), Tatlas::tp, Tchart::w, and Warning(). Referenced by AtlasAStar(), and AtlasGBF().
Searches for charts close to the current one, determines if they are actually neighbours (close enough and with similar tangent spaces) and crops the two charts so that they do not overlap. The crop is performed in the polytope bounding the chart ball (defined in tangent space). This is typically used for chart generated from other charts (using ExtendAtlasTowardPoint or ExtendAtlasFromPoint). In those cases the new chart center is close to its parent chart and there must be and intersection between the parent and the child. If there is not an error is triggered. When charts are generated in this hierarchical fashion, we only check for singularities in the transitions between parents and children. This save many checks but still ensures that singularities will be detected. However, this function can also be used for a chart generated from a point not necessaritly close to any other chart (i.e. for a new chart with not known parent). In this case no error is triggered is the chart does not intersect with any special chart. Moreover, in this case we check for singularity detection in any neighgouring relation. We assume that the chart 'cmID' has never been checked for intersection with the rest of the atlas.
Definition at line 1547 of file atlas.c. References AddChart2Btree(), Tatlas::ambient, ChartNumNeighbours(), Tatlas::charts, CT_DETECT_BIFURCATIONS, Tatlas::currentChart, DetectBifurcation(), Error(), FALSE, GetParameter(), IntersectCharts(), Tatlas::n, NO_UINT, SearchInBtree(), Tatlas::tp, and TRUE. Referenced by PostProcessNewCharts().
Approximates the geodesic distance between the centers of two charts by computing intermediated points from the center of the parent chart to the center of the child chart. If the path between the two chart centers is blocked by obstacles the return is inf. The steps are taken by linear interpolation between the chart centers and the projecting to the manifold via Newton. We do not use the tangent space at the parent chart to do the parametrization since its validity area might not reach the center of the child. If in any of the intermediate steps we did not manage to determine a point on the manifold the process is stopped and the return is inf (meaining it is not posssible to directly connect the two chart centers.
Definition at line 1627 of file atlas.c. References Tatlas::charts, CS_WD_IN_COLLISION, CS_WD_NEWTON_IN_SIMP, CT_DELTA, DifferenceVectorTopology(), DistanceTopology(), DIVERGED, FALSE, GetChartCenter(), GetParameter(), INF, Tatlas::m, Tatlas::n, NEW, Newton2ManifoldPlane(), SumVectorScale(), Tatlas::tp, TRUE, and Tatlas::w. Referenced by AtlasAStar().
Adds the Hessian to the atlas, computed from the simbolic Jacobian. The Hessian is used to deal with singularities. This function must be used after the simbolic Jacobian has been defined.
Releases the Hessian information stored by ComputeAtlasHessian.
Initializes the topology array in the atlas.
Definition at line 2652 of file atlas.c. References CS_WD_GET_SIMP_TOPOLOGY, Error(), FALSE, Tatlas::m, TOPOLOGY_S, Tatlas::tp, and Tatlas::w. Referenced by InitAtlas(), and LoadAtlas().
Determines if there is a bifurcation between the center of two charts. This process potentially generates a set of new bifurcations that are latter processed using ProcessBifurcation.
Definition at line 1731 of file atlas.c. References Tatlas::bifurcation, Tatlas::charts, Tbifurcation::d1, Tbifurcation::d2, FALSE, GetChartDegree(), GetChartTangentSpace(), Tatlas::J, Tatlas::mBifurcations, MEM_DUP, Tbifurcation::mID1, Tbifurcation::mID2, Tatlas::nBifurcations, NEW, Tbifurcation::p, and SingularChart(). Referenced by AddTrustedChart2Atlas(), and DetermineChartNeighbours().
Once a bifurcation is detected, we have to determine the singular point, i.e., the point where the bifurcation actually occur. If found, the point is stored in the corresponding bifurcation structure. Note that since all our procedures are accurate up to epsilon, the singular point is not actually found, but we find an approximation of it. This means that at the returned point the Jacobian is not perfectly singular (but close to be singular). This is one of the steps executed in the ProcessBifurcation procedure.
Definition at line 1776 of file atlas.c. References Tatlas::ambient, Tatlas::bifurcation, Tatlas::ce, Chart2Manifold(), Tatlas::charts, CompareTangentSpaces(), CT_EPSILON, Tbifurcation::d1, Tbifurcation::d2, DeleteChart(), DifferenceVector(), Tatlas::e, Error(), FALSE, GetChartCenter(), GetChartDegree(), GetChartTangentSpace(), GetParameter(), InitPossiblySingularChart(), Tatlas::J, Tatlas::k, Tatlas::m, Manifold2Chart(), Tbifurcation::mID1, Tbifurcation::mID2, MinCosinusBetweenCharts(), NEW, Tbifurcation::p, Tatlas::r, Tatlas::simpleChart, SingularChart(), SumVectorScale(), Tatlas::tp, TRUE, and Tatlas::w. Referenced by ProcessBifurcation().
This function was intented as a replacement of FindSingularPoint with the idea of defining the singular points analytically and using a Newton process to avoid the slow dicotomic search in FindSingularPoint. However, the Newton process does not converge to the singularity unless we start the process very close to it (and even in this case it is many times divergent). Thus we reformulate this function as a refinement of the singular point localization implemented in FindSingularPoint. Note that this function is not actually used but we keep it because we expended a lot of effort in its implementation and it could be actually useful if we ever improve it. For instance, if this function worked properly, we could save the use of FindRightNullVector since the lambda part of the solution found (but not used by this function) is the new right null vector now determined in FindRightNullVector If this function is finally removed from the code we can also remove ComputeAtlasHessian, DeleteAtlasHessian and the H fiel of Tatlas.
Definition at line 1921 of file atlas.c. References AllocateHessianEvaluation(), ArrayPi2Pi(), Tatlas::bifurcation, Tatlas::charts, CS_WD_EVALUATE_SIMP_EQUATIONS, CT_EPSILON, CT_MAX_NEWTON_ITERATIONS, DeleteNewton(), EvaluateHessian(), EvaluateJacobianInVector(), EvaluateTransposedJacobianInVector(), FALSE, FindKernel(), FreeHessianEvaluation(), GeneralDotProduct(), GetChartCenter(), GetChartTangentSpace(), GetColumn(), GetNewtonMatrixBuffer(), GetNewtonRHBuffer(), GetParameter(), Tatlas::H, InitHessian(), InitNewton(), Tatlas::J, Tatlas::k, Tatlas::m, MatrixVectorProduct(), Tbifurcation::mID1, Tatlas::ncJ, NEW, NewtonStep(), Norm(), Tatlas::nrJ, Tbifurcation::p, RC2INDEX, SubMatrixFromMatrix(), SubMatrixFromTMatrix(), TMatrixVectorProduct(), Tatlas::tp, TRUE, and Tatlas::w.
Finds the right null vector that does not belong to the tangent space. We basically compute a basis of the kernel of the Jacobian at the singular point. If theory (when the perfectly determined the singular point) the kernel will have dimension k+1. In practice we have dimension k plus one vector corresponding to a small (but not zero) eigenvalue. The kernel vectors (plus the addiontal one) can be determined finding the lowest eigenvalues (or value of the diagonal of R assuming as 0 those not present). We proceed as when computing the kernel of a Jacobian and we check for each candiate to belong to the basis of the kernel if it is aligned with the provided tangent space (an approximation of the tangent space at the singularity). We return the less aligned vector.
Definition at line 2137 of file atlas.c. References Tatlas::bifurcation, Tatlas::charts, ColumnSquaredNorm(), Error(), EvaluateTransposedJacobianInVector(), FindKernel(), GetChartTangentSpace(), GetColumn(), INF, Tatlas::J, Tatlas::k, Tatlas::m, Tbifurcation::mID1, Tatlas::ncJ, NEW, Tatlas::nrJ, Tbifurcation::p, PrintMatrix(), PrintTMatrix(), TMatrixMatrixProduct(), and TRUE. Referenced by ProcessBifurcation().
Once we detected a bifurcation point (DetectBifurcation), we precisely locate it (FindSingularPoint) and we have the additional vector of the null space of the Jacobian (FindRightNullVector), we have now to locate a point in the other branch manifold. To do it, we move in the from the singular point in the direction of the new vector of the Jacobian kernel basis. This generates a point away from the current manifold branch (which localy is close to the tangent space at the bifrucation that is approximated by the tangent space on one of the points used to detect the singular point). From this point we try to reach the manifold but moving on a sub-space parallel to the tangent space of the for the known manifold branch. In this way we maximize the probability of reaching the other manifold branch. The solution point should be on the manifold ( This procedure does not works alwasy but is is simple and works in many cases.
Definition at line 2349 of file atlas.c. References Tatlas::bifurcation, DistanceTopology(), Error(), FALSE, Tatlas::m, NEW, Newton2ManifoldPlane(), Tbifurcation::p, Tatlas::r, SumVectorScale(), and Tatlas::tp. Referenced by ProcessBifurcation().
When we detecta a bifurcation, we define two charts, one at the current branch of the variety, and one at the new branch. These two charts are related so that we can eventually cross the singularity without jumps when planning. This is typically the final step of ProcessBifurcation but we can use it as soon as we identify a point in the new branch of the variety (this can happen in the process of finding the bifurcation point).
Definition at line 2392 of file atlas.c. References Tatlas::ambient, Tatlas::bifurcation, Tatlas::ce, Tatlas::charts, Tatlas::currentChart, Tatlas::e, Error(), FALSE, GetChartTangentSpace(), InitChartWithTangent(), InitSingularChart(), Tatlas::J, Tatlas::k, LinkCharts(), Tatlas::m, Tatlas::maxCharts, MEM_DUP, Tbifurcation::mID1, MinCosinusBetweenCharts(), NEW, NewSmallAngleAtBifurcation(), NO_UINT, Tbifurcation::p, PostProcessNewCharts(), Tatlas::r, Tatlas::tp, Tatlas::w, and Warning(). Referenced by ProcessBifurcation().
Processes the bifurcation points generated in the last calls to DetectBifurcation that are not yet processed. This amounts to detect the singular point in between the two chart centers, to generate a chart in the other branch of the manifold, and to search for its neighbours.
Definition at line 2444 of file atlas.c. References DefineChartsAtBifurcation(), FindPointInOtherBranch(), FindRightNullVector(), FindSingularPoint(), NewBifurcation(), NewNoJumpBranch(), NewNoSingularEnough(), NewSingularPointMissed(), and Tatlas::npBifurcations. Referenced by PostProcessNewCharts().
Loads the bifurcation information from a file.
Definition at line 2493 of file atlas.c. References Tatlas::bifurcation, Tbifurcation::d1, Tbifurcation::d2, Tatlas::m, Tatlas::mBifurcations, Tbifurcation::mID1, Tbifurcation::mID2, Tatlas::nBifurcations, NEW, Tatlas::npBifurcations, and Tbifurcation::p. Referenced by LoadAtlas().
Saves the bifurcation information to a file.
Definition at line 2523 of file atlas.c. References Tatlas::bifurcation, Tbifurcation::d1, Tbifurcation::d2, Tatlas::m, Tatlas::mBifurcations, Tbifurcation::mID1, Tbifurcation::mID2, Tatlas::nBifurcations, Tatlas::npBifurcations, and Tbifurcation::p. Referenced by SaveAtlas().
Plots a red line connecting the chart center that are at the two sides of a bifurcation.
Definition at line 2546 of file atlas.c. References Tatlas::bifurcation, Tatlas::charts, Close3dObject(), CS_WD_REGENERATE_ORIGINAL_POINT, DeleteColor(), GetChartCenter(), Tbifurcation::mID1, Tbifurcation::mID2, Tatlas::nBifurcations, NewColor(), PlotVect3d(), StartNew3dObject(), and Tatlas::w.
Deletes the bifurcation information stored in the atlas.
Definition at line 2583 of file atlas.c. References Tatlas::bifurcation, Tatlas::mBifurcations, Tatlas::nBifurcations, Tatlas::npBifurcations, and Tbifurcation::p. Referenced by DeleteAtlas().
Tries to expand the atlas from a given point defined on the chart tangent space. This point is assumed to be on the border of the atlas (on the ball defined in the given chart and not in any other ball from other charts). If the new chart can not be properly defined, the we try to try to generate it closer to the center of the parent chart. When very close to the parent chart center we are supposed to be able to generate a new chart without any issues.
Definition at line 1015 of file atlas.c. References AddBorderConstraint(), Tatlas::ambient, Tatlas::ce, Chart2Manifold(), ChartIsFrontier(), Tatlas::charts, CloseCharts(), CollisionChart(), CS_WD_IN_COLLISION, CS_WD_SIMP_INEQUALITIES_HOLD, CT_EPSILON, Tatlas::currentChart, DeleteChart(), Tatlas::e, Error(), FALSE, GetParameter(), InitChart(), Tatlas::J, Tatlas::k, Tatlas::m, Tatlas::maxCharts, MEM_DUP, MIN_SAMPLING_RADIUS, NEW, NewAtlasExtension(), NewDecompositionError(), NewFarFromParent(), NewGoodExtension(), NewImpossible(), NewLargeError(), NewNonRegularPoint(), NewNotInManifold(), NewRadiousChange(), NewSingularImpossible(), NO_UINT, Norm(), PointInBoxTopology(), PostProcessNewCharts(), Tatlas::r, SAMPLING_RADIUS_REDUCTION_FACTOR, ScaleVector(), Tatlas::simpleChart, SingularChart(), Tatlas::tp, TRUE, and Tatlas::w. Referenced by AtlasAStar(), and BuildAtlasFromPoint().
This is like ExtendAtlasFromPoint but the process is started close to the center of the parent chart and the new chart is progressively generated towards the targed point as we have success in generating the new chart. In this process, we could even go further that the targed point. Another difference with ExtendAtlasFromPoint is that here we take into account obstacles.
Definition at line 1246 of file atlas.c. References Tatlas::ambient, Tatlas::ce, Chart2Manifold(), Tatlas::charts, CloseCharts(), CollisionChart(), CT_DELTA, CT_EPSILON, Tatlas::currentChart, DeleteChart(), Tatlas::e, Error(), FALSE, GetChartCenter(), GetChartRadius(), GetParameter(), InitChart(), Tatlas::J, Tatlas::k, Tatlas::m, Tatlas::maxCharts, MEM_DUP, NEW, NewAtlasExtension(), NewDecompositionError(), NewFarFromParent(), NewGoodExtension(), NewImpossible(), NewInCollision(), NewLargeError(), NewNonRegularPoint(), NewNotInManifold(), NewRadiousChange(), NewSingularImpossible(), Norm(), PostProcessNewCharts(), Tatlas::r, ScaleVector(), Tatlas::simpleChart, SingularChart(), Tatlas::tp, TRUE, and Tatlas::w. Referenced by AtlasGBF().
Determines a point in the intersection of a given plane and the manifold. This is an auxiliary function of FindPointInOtherBranch but it is also used when defining an (Atlas)RRT (to incrementally extend a branch of the tree toward a given point). The point is searched using a Newton procedure where the syste of equations defining the manifold is extended with the equation defining the given plane.
Definition at line 2250 of file atlas.c. References ArrayPi2Pi(), CS_WD_EVALUATE_SIMP_EQUATIONS, CT_EPSILON, CT_MAX_NEWTON_ITERATIONS, DeleteNewton(), Error(), EvaluateJacobianInVector(), FALSE, GetNewtonMatrixBuffer(), GetNewtonRHBuffer(), GetParameter(), InitNewton(), Tatlas::J, Tatlas::m, Tatlas::n, Tatlas::ncJ, NewtonStep(), Norm(), Tatlas::nrJ, SetRow(), Tatlas::tp, TRUE, and Tatlas::w. Referenced by FindPointInOtherBranch(), and GeodesicDistance().
Defines a new atlas heap element.
Definition at line 2600 of file atlas.c. References TAtlasHeapElement::beta, TAtlasHeapElement::chartID, TAtlasHeapElement::cost, Error(), and TAtlasHeapElement::nPenalized. Referenced by AtlasAStar(), AtlasGBF(), and BuildAtlasFromPoint().
Defines a new atlas heap element from another. We use void pointers to use the generic heap implementation.
Definition at line 2610 of file atlas.c. Referenced by AtlasAStar(), AtlasGBF(), and BuildAtlasFromPoint().
Gets the chart identifer stored in an atlas heap element.
Definition at line 2618 of file atlas.c. References TAtlasHeapElement::chartID. Referenced by AtlasAStar(), AtlasGBF(), and BuildAtlasFromPoint().
Gets the cost stored in an atlas heap element.
Definition at line 2623 of file atlas.c. References TAtlasHeapElement::cost.
Identifies atlas heap element with lower cost.
Definition at line 2628 of file atlas.c. Referenced by AtlasAStar(), AtlasGBF(), and BuildAtlasFromPoint().
Penalizes the cost of the atlas heap element. Every time this function is called we increase the counter in the heap element and, thus, we penalize the cost accordingly. The idea is that charts where it is difficult to sample should be penalized to deviate the search to neighbouring charts with larger external border.
Definition at line 2643 of file atlas.c. References TAtlasHeapElement::nPenalized. Referenced by AtlasGBF().
Releases the memory alloated in the atlas heap element, if any.
Definition at line 2648 of file atlas.c. Referenced by AtlasAStar(), AtlasGBF(), and BuildAtlasFromPoint().
Initializes an empty atlas.
Definition at line 2676 of file atlas.c. References Tatlas::ambient, Tatlas::bifurcation, Tatlas::ce, Tatlas::charts, CS_WD_GENERATE_SIMP_INITIAL_BOX, CS_WD_GET_SIMP_JACOBIAN, CS_WD_INIT_CD, Tatlas::currentChart, Tatlas::e, FALSE, GetJacobianSize(), Tatlas::H, INIT_NUM_BIFURCATIONS, INIT_NUM_CHARTS, Tatlas::J, Tatlas::k, Tatlas::m, Tatlas::maxCharts, Tatlas::mBifurcations, Tatlas::n, Tatlas::nBifurcations, Tatlas::ncJ, Tatlas::nCores, NEW, Tatlas::npBifurcations, Tatlas::npCharts, Tatlas::nrJ, Tatlas::parallel, Tatlas::r, SetAtlasTopology(), Tatlas::simpleChart, and Tatlas::w. Referenced by InitAtlasFromPoint().
Initializes an atlas defining a local chart from a given point. If the given point is not on the manifold nothing is added to the atlas.
Definition at line 2742 of file atlas.c. References Tatlas::ambient, Tatlas::ce, ChangeParameter(), Tatlas::charts, CS_WD_GENERATE_SIMPLIFIED_POINT, CS_WD_ORIGINAL_IN_COLLISION, CS_WD_REGENERATE_SOLUTION_POINT, CT_CE, CT_E, CT_EPSILON, CT_N_DOF, CT_R, Tatlas::currentChart, Tatlas::e, Error(), EvaluateTransposedJacobianInVector(), FindRank(), FrontierChart(), GetParameter(), InitAtlas(), InitBTree(), InitChart(), Tatlas::J, Tatlas::k, Tatlas::m, Tatlas::ncJ, NEW, Tatlas::npCharts, Tatlas::nrJ, Tatlas::r, Tatlas::simpleChart, Tatlas::tp, Tatlas::w, and Warning(). Referenced by BuildAtlasFromPoint(), InitAtlasRRT(), main(), and MinimizeOnAtlas().
Defines a chart on the given point and adds it to the atlas updating the neighbouring relations and checking for the presence of singularities in between the centers of the charts dectected as neighbours, if any. Note that we could actually build an atlas by sampling random points on the manifold and using this function to create new charts until the atlas is compleated. However this estrategy is not guaranteed be be succesful and could produce atlas with charts for very different sizes. This is why higher dimensional continuation typically uses more principled ways to generate new charts from the existing ones (see BuildAtlasFromPoint).
Definition at line 2836 of file atlas.c. References Tatlas::ambient, Tatlas::ce, Tatlas::charts, Tatlas::currentChart, Tatlas::e, FALSE, InitChart(), Tatlas::J, Tatlas::k, Tatlas::m, Tatlas::maxCharts, MEM_DUP, NEW, NO_UINT, PostProcessNewCharts(), Tatlas::r, Tatlas::simpleChart, Tatlas::tp, TRUE, and Tatlas::w. Referenced by MinimizeOnAtlas().
Version of AddChart2Atlas for atlas in AtlasRRT (construction of a RRT from an atlas and the reverse). In this special version, we add the chart to the atlas and we determine its neighbours but without any concern about detecting singularities nor enforcing intersection with the parent chart. Moreover, we trust that the input point is in the manifold and that its is collision free (these conditions are checked when generating the point).
Definition at line 2870 of file atlas.c. References Tatlas::ambient, Tatlas::ce, Tatlas::charts, CT_DETECT_BIFURCATIONS, Tatlas::currentChart, DetectBifurcation(), Tatlas::e, FALSE, GetParameter(), InitTrustedChart(), Tatlas::J, Tatlas::k, Tatlas::m, Tatlas::maxCharts, MEM_DUP, Tatlas::n, NEW, NO_UINT, PostProcessNewCharts(), Tatlas::r, Tatlas::simpleChart, Tatlas::tp, and Tatlas::w. Referenced by AddChart2AtlasRRT().
Defines an atlas from a given point and covering the whole connected component including this point. This procedure can be quite time demanding for high-dimensional manifolds. For these cases, we implement a parallel version (via MP). However, currently the parallel version can not deal with obstacles (i.e., it can only run on cuik files but not on world files).
Definition at line 2919 of file atlas.c. References AddElement2Heap(), BoundaryPointFromExternalCorner(), Tatlas::charts, CopyAtlasHeapElement(), CT_ATLASGBF_BETA, CT_MAX_CHARTS, CT_N_DOF, Tatlas::currentChart, DeleteAtlasHeapElement(), DeleteHeap(), DistanceTopology(), Error(), ExtendAtlasFromPoint(), ExtractMinElement(), FALSE, GetAtlasHeapElementID(), GetChartCenter(), GetParameter(), HeapEmpty(), INIT_NUM_CHARTS_IN_ATLAS_HEAP, InitAtlasFromPoint(), InitAtlasHeapElement(), InitAtlasStatistics(), InitHeap(), Tatlas::k, LessThanAtlasHeapElement(), Tatlas::m, Tatlas::maxCharts, MEM_DUP, Tatlas::nCores, NEW, NewBoundaryAttempt(), NewChartFromPoint(), NewNotInBoundary(), NO_UINT, OpenChart(), Tatlas::parallel, PostProcessNewCharts(), PrintAtlasStatistics(), randomDouble(), RANDOMNESS, Tatlas::tp, TRUE, and WrongCorner(). Referenced by main().
Local minimization of a cost function defined on the atlas. The minimization is done using gradient descent. The gradient is numerically evaluated. The presence of bifurcation si taken into account (if the appropiate parameteres are set, see CT_DETECT_BIFURCATIONS) and, thus, different minima can be determined. The paths to the minima are stored in separate files.
Definition at line 3106 of file atlas.c. References AddChart2Atlas(), AddSample2Samples(), ChangeParameter(), Chart2Manifold(), Tatlas::charts, CS_WD_GET_SYSTEM_VARS, CS_WD_REGENERATE_ORIGINAL_POINT, CT_DELTA, CT_DETECT_BIFURCATIONS, CT_EPSILON, CT_N_DOF, Tatlas::currentChart, Error(), FALSE, GetChartCenter(), GetParameter(), INF, InitAtlasFromPoint(), InitSamples(), Tatlas::J, Tatlas::m, MEM_DUP, TMinTrace::nc, NEW, Norm(), TMinTrace::ns, SaveSamples(), SaveSamplesN(), ScaleVector(), TMinTrace::st, TRUE, Tatlas::w, and Warning(). Referenced by main().
Returns the maximum curvature error for all the charts, i.e., the maximum angle between neighbouring charts.
Definition at line 3321 of file atlas.c. References Tatlas::ce.
Expands the atlas with the purpose to reach a given configuration using a A* search strategy.
< Predecesor. Previou node in the best path to the start node. Definition at line 3341 of file atlas.c. References AddElement2Heap(), ATLAS_VERBOSE, BoundaryPointFromExternalCorner(), ChartNeighbourID(), ChartNumNeighbours(), Tatlas::charts, CopyAtlasHeapElement(), TAStarInfo::cost, CS_WD_ERROR_IN_SIMP_EQUATIONS, CS_WD_GENERATE_SIMPLIFIED_POINT, CS_WD_GET_SYSTEM_VARS, CS_WD_ORIGINAL_IN_COLLISION, CS_WD_REGENERATE_SOLUTION_POINT, CT_ATLASGBF_BETA, CT_EPSILON, CT_MAX_CHARTS, CT_MAX_PLANNING_TIME, Tatlas::currentChart, DeleteAtlasHeapElement(), DeleteHeap(), DeleteStatistics(), DistanceOnChart(), DistanceTopology(), Error(), ExpandibleChart(), ExtendAtlasFromPoint(), ExtractMinElement(), FALSE, GeodesicDistance(), GetAtlasHeapElementID(), GetChartCenter(), GetElapsedTime(), GetHeapElement(), GetParameter(), HeapEmpty(), HeapSize(), TAStarInfo::heuristic, INF, INIT_NUM_CHARTS_IN_ATLAS_HEAP, InitAtlasHeapElement(), InitAtlasStatistics(), InitHeap(), InitStatistics(), Tatlas::J, Tatlas::k, LessThanAtlasHeapElement(), Tatlas::m, Tatlas::maxCharts, MEM_DUP, MEM_EXPAND, Tatlas::n, Tatlas::nCores, NEW, NewBoundaryAttempt(), NewChartFromPoint(), NewNotInBoundary(), NO_UINT, ON_CUIKSYSTEM, Tatlas::parallel, PointOnChart(), PostProcessNewCharts(), PrintAtlasStatistics(), ReconstructAtlasPath(), TAStarInfo::status, Tatlas::tp, TRUE, Tatlas::w, Warning(), and WrongCorner(). Referenced by main().
Expands the atlas with the purpose to reach a given configuration using a Greedy Best First search strategy.
Definition at line 3677 of file atlas.c. References AddElement2Heap(), ATLAS_VERBOSE, Tatlas::charts, CopyAtlasHeapElement(), CS_WD_ERROR_IN_SIMP_EQUATIONS, CS_WD_GENERATE_SIMPLIFIED_POINT, CS_WD_GET_SYSTEM_VARS, CS_WD_ORIGINAL_IN_COLLISION, CS_WD_REGENERATE_SOLUTION_POINT, CT_ATLASGBF_BETA, CT_EPSILON, CT_MAX_CHARTS, CT_MAX_PLANNING_TIME, Tatlas::currentChart, DeleteAtlasHeapElement(), DeleteHeap(), DeleteStatistics(), DistanceOnChart(), DistanceTopology(), Error(), ExpandibleChart(), ExtendAtlasTowardPoint(), ExtractMinElement(), FALSE, GetAtlasHeapElementID(), GetChartCenter(), GetElapsedTime(), GetParameter(), HeapEmpty(), INF, INIT_NUM_CHARTS_IN_ATLAS_HEAP, InitAtlasHeapElement(), InitAtlasStatistics(), InitHeap(), InitStatistics(), Tatlas::J, Tatlas::k, LessThanAtlasHeapElement(), Tatlas::m, Tatlas::maxCharts, MEM_EXPAND, Tatlas::n, Tatlas::nCores, NEW, NewBoundaryAttempt(), NewNotInBoundary(), NO_UINT, PenalizeAtlasHeapElement(), PointOnChart(), PrintAtlasStatistics(), RandomPointOnBoundary(), ReconstructAtlasPath(), Tatlas::tp, TRUE, Tatlas::w, and Warning(). Referenced by main().
Returns the approximated memory used (in bytes) by a given atlas.
Definition at line 3831 of file atlas.c. References ChartMemSize(), Tatlas::charts, and Tatlas::currentChart. Referenced by AtlasRRTMemSize(), and main().
Stores all the information in the atlas in a file.
Definition at line 3842 of file atlas.c. References Tatlas::ce, Tatlas::charts, Tatlas::currentChart, Tatlas::e, Error(), GetFileFullName(), Tatlas::k, Tatlas::m, Tatlas::maxCharts, Tatlas::n, Tatlas::r, SaveBifurcations(), SaveChart(), and Tatlas::simpleChart. Referenced by main(), and SaveAtlasRRT().
Construct an atlas from the information previously stored in a file by SaveAtlas.
Definition at line 3869 of file atlas.c. References AddChart2Btree(), Tatlas::ambient, Tatlas::ce, Tatlas::charts, CS_WD_GENERATE_SIMP_INITIAL_BOX, CS_WD_GET_SIMP_JACOBIAN, Tatlas::currentChart, Tatlas::e, Error(), FALSE, GetFileFullName(), GetJacobianSize(), Tatlas::H, InitBTree(), Tatlas::J, Tatlas::k, LoadBifurcations(), LoadChart(), Tatlas::m, Tatlas::maxCharts, Tatlas::n, Tatlas::ncJ, Tatlas::nCores, NEW, Tatlas::nrJ, Tatlas::parallel, Tatlas::r, SetAtlasTopology(), Tatlas::simpleChart, Tatlas::tp, and Tatlas::w. Referenced by LoadAtlasRRT(), and main().
Returns the number of charts in the atlas.
Definition at line 3931 of file atlas.c. References Tatlas::currentChart. Referenced by AddChart2AtlasRRT(), InitAtlasRRT(), main(), and RandomPointInAtlasTree(). Returns a pointer to one of the charts of the atlas. Care should be taken not to manipulate the chart (use it for query only).
Definition at line 3936 of file atlas.c. References Tatlas::charts. Referenced by AddBranchToAtlasRRT(), AddChart2AtlasRRT(), AddSample2AtlasRRT(), AtlasRRT(), AtlasRRTSample(), GetRRTNNInNeighbourChart(), NewTemptativeSample(), PlotAtlasRRT(), PlotQrand(), PointTowardRandSample(), PopulateWithSamples(), PrintAtlasRRTStatistics(), and RandomPointInAtlasTree().
Samples a random point on the part of the manifold covered by the atlas with uniform distribution. We select a chart with uniform distribution and then a point in the tangent space of the selected chart.
Definition at line 3944 of file atlas.c. References Tatlas::charts, Tatlas::currentChart, randomMax(), RandomPointInChart(), randomWithDistribution(), and Tatlas::tp. Referenced by RandomPointInAtlasTree().
Approximates the volume of the manifold parametrized by an atlas.
Definition at line 3966 of file atlas.c. References Tatlas::charts, ChartVolume(), Tatlas::currentChart, FrontierChart(), Tatlas::J, and Tatlas::tp. Referenced by main().
Stores the centers of the charts in the form of boxes.
Definition at line 3987 of file atlas.c. References Chart2Manifold(), ChartNeighbourID(), ChartNumNeighbours(), Tatlas::charts, CreateFileName(), CS_WD_GET_SYSTEM_VARS, CS_WD_REGENERATE_ORIGINAL_POINT, Tatlas::currentChart, DeleteFileName(), Error(), FrontierChart(), GetChartCenter(), GetFileFullName(), INF, Tatlas::J, Tatlas::k, Tatlas::m, Manifold2Chart(), NEW, NO_UINT, ScaleVector(), SOL_EXT, SOL_WITH_DUMMIES_EXT, Tatlas::tp, and Tatlas::w. Referenced by main().
Stores the centers of the singular charts in the form of boxes.
Definition at line 4095 of file atlas.c. References Tatlas::charts, CreateFileName(), CS_WD_GET_SYSTEM_VARS, CS_WD_REGENERATE_ORIGINAL_POINT, Tatlas::currentChart, DeleteFileName(), Error(), GetChartCenter(), GetFileFullName(), SingularChart(), SOL_EXT, SOL_WITH_DUMMIES_EXT, and Tatlas::w. Referenced by main().
Plots a 3d projection of an atlas defined on a manifold. Although the ambien space can have arbitrary dimension we project it on 3 dimensions. Only 2D manifolds plots can be properly visualized. The output plot can be visualized using geomview.
Definition at line 4151 of file atlas.c. References ChartNeighbourID(), ChartNumNeighbours(), Tatlas::charts, Close3dObject(), Close3dObjectNoColor(), ClosePlot3d(), CS_WD_REGENERATE_ORIGINAL_POINT, Tatlas::currentChart, Delete3dObject(), DeleteColor(), ExpandibleChart(), FALSE, FrontierChart(), GetChartCenter(), InitPlot3d(), Tatlas::J, Tatlas::k, NewColor(), NO_UINT, PLOT_AS_POLYGONS, PLOT_ATLAS_IN_COLORS, PlotChart(), PlotVect3d(), Tatlas::simpleChart, SingularChart(), StartNew3dObject(), and Tatlas::w. Referenced by main(), and PlotAtlasRRT().
Plots a 3d projection of triangular mesh formed by the atlas centers. This is only well defined for surfaces, i.e., for manifolds of dimension 2. The difference with PlotAtlas is that here only the chart centers are used and, thus, the charts are not displayed. The use of a triangular mesh on the chart centers results in a smoother visualization. The plot generated with PlotAtlas creates a separate polytope for each atlas and, thus there are "discontinuities" in between charts. The triangular mesh is fully continuous and can be properly smoothed and shaded. Although the ambien space can have arbitrary dimension we project it on 3 dimensions. The output plot can be visualized using geomview.
Definition at line 4314 of file atlas.c. References Tatlas::charts, Close3dObject(), ClosePlot3d(), CostColor(), CrossProduct(), CrossTopologyBorder(), CS_WD_GET_VAR_TOPOLOGY, CS_WD_REGENERATE_ORIGINAL_POINT, CT_CUT_X, CT_CUT_Y, CT_CUT_Z, CT_REPRESENTATION, Tatlas::currentChart, DifferenceVector(), DotProduct(), Error(), FALSE, GetChartCenter(), GetChartNeighboursFromVertices(), GetParameter(), InitPlot3d(), Tatlas::k, M_2PI, MEM_DUP, NeighbouringTriangles(), NEW, NewColor(), NO_UINT, Plot3dObject(), Plot3dObjectWithColors(), REP_JOINTS, SameTriangle(), ScaleVector(), StartNew3dObject(), TOPOLOGY_R, TRUE, and Tatlas::w. Referenced by main().
Deletes the information stored in the atlas.
Definition at line 4561 of file atlas.c. References Tatlas::ambient, Tatlas::charts, Tatlas::currentChart, DeleteBifurcations(), DeleteBox(), DeleteBTree(), DeleteChart(), DeleteHessian(), DeleteJacobian(), Tatlas::H, Tatlas::J, and Tatlas::tp. Referenced by DeleteAtlasRRT(), and main(). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
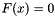) and should be in the kernel of the Jacobian at the singular point ( 
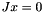). When solving this using Newton we have a matrix A with two Jacobians, one at the current point and another at the singularity (actually we have one basis of the Jacobian at the bifurcation point and a full Jacobian, possibly with redundant equations, at the current point).
Follow us!