Research line

Computational Robotics

Computational Robotics Image

The COMPUTATIONAL ROBOTICS Group investigates the theoretical, computational, and implementation aspects that arise in the design, construction, motion planning, and control of complex robotic systems. Among these we find serial, parallel, or locomotive robots, intelligent prostheses, biomechanical support systems for movement or rehabilitation, or other robots that, due to their sensory and compliance capacities,
can safely interact with humans in an agile manner.

Head of line: Alba Perez Gracia

Head of line

Tech. transfer

Our activity finds applications in several fields through collaboration with our technological partners

Research projects

We carry out projects from national and international research programmes.
→ More about our research projects

<< Back to Computational Robotics main page

Robot design and construction

The group designs and constructs innovative mechatronic devices based mainly on parallel architectures. Our developments include the “Wrenchpad” (a six-axis tactile pad), several tensegrity-based robots, a pentaglide, several variations of the Gough-Stewart platform, different cable-driven robots, and the "Scherbot" robot (a five-bar mechanism to test kinodynamic motion planning and control techniques to cross singularities). The group also works on the development of various reconfigurable robots. These offer the possibility of reducing the number of actuators needed to perform a task, with the consequent decrease in construction costs. Moreover, reconfigurations can also be used to enlarge the robot’s workspace, or to avoid problematic configurations like singularities.

Research area 1 of CRG

Computational kinematics and dynamics

In this area, the group develops novel methods for the position analysis of multibody systems. The problem consists of finding all possible configurations that a multibody system can adopt while respecting the kinematic constraints imposed by its joints. The techniques can be applied to robotics (in contexts like direct or inverse kinematics, cooperative manipulation, grasping, or motion planning), structural biology (e.g., to conformational analysis of biomolecules), or multibody dynamics (initial position and finite displacement problems). The group works using two approaches: one based on relaxation techniques, and the other based on characteristic polynomials using Distance Geometry. Many of the developments are implemented in the CUIK suite, a large toolbox for motion analysis and synthesis of closed-chain multibody systems. The group also has expertise on advanced dynamics algorithms based on Clifford or Spatial Vector algebras, as well as on advanced methods of simulation of constrained dynamical systems through integration on manifolds.

Research area 2 of CRG

Singularity analysis

Singularities play a prominent role for understanding the configuration space of a robot. Depending on their nature, they give rise to overspeeding problems, dexterity losses, or controllability issues. Thus, these configurations are often avoided during the usual operation of a robot, especially in applications that require careful human-robot interactions. Singularities, however, may also give rise to mechanical advantage (e.g., they can be used to transform small motor torques into large end-effector forces) and also provide the boundary of the workspace, which is a crucial information for the robot designer. The group has developed new geometric and computational tools that allow characterizing the singularity loci of a robot, either for specific classes of robots, or for general multibody systems. New algorithms for controlling the motions across forward singularities have been developed as well, which allow the extension of the reachable workspace in parallel mechanisms.

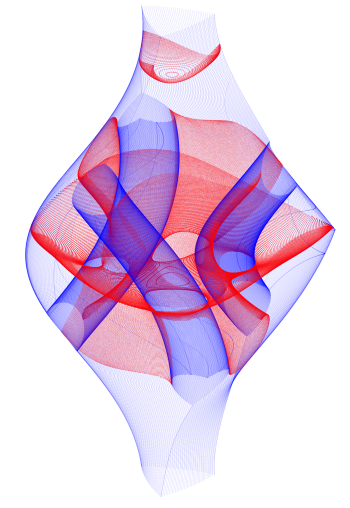
Research area 3 of CRG

Motion planning and control

Along this line, the group develops algorithms for the planning and control of motions of general multibody systems. These systems may involve holonomic or nonholonomic constraints, like loop-closure, contact, or rolling constraints. The goal is to design feasible trajectories bringing the robot to a desired state without colliding with obstacles, and to obtain robust controllers to track the trajectories in practice. Several techniques have been developed to both ends, which consider the kinematic constraints of the robot, or also its full dynamic model (including motor saturations and speed limits). In both cases, innovative methods based on higher-dimensional continuation and randomized sampling techniques have been proposed for the planning of motions. These motions are further refined using trajectory optimization methods. The control of motions, in turn, is achieved by means of numerical optimal control techniques. The group has expertise on applying these techniques to fixed-base manipulators, mobile platforms of various sorts (omnidirectional, nonholonomic, or inverted-pendulum ones), cable driven robots, or flying drones. The group has also investigated the connections with related problems in biochemistry, contributing with novel algorithms for finding low-energy paths between molecular conformations.

Research area 4 of CRG

These are the latest research projects of the Computational Robotics research line:

These are the most recent publications (2025 - 2024) of the Computational Robotics

  • M. Stevanovic, N. Tagkalidou, C.R. Multisanti, S. Pujol, O. Aljabasini, E. Prats, C. Faggio, J.M. Porta, C. Barata and D. Raldúa. Zebra_K, a kinematic analysis automated platform for assessing sensitivity, habituation and prepulse inhibition in adult zebrafish. Science of the Total Environment, 958: 178028, 2025.

    Open/Close abstract Abstract Info Info pdf PDF

  • F. Thomas. Fixed points in distance recurrence formulas, 19th International Symposium on Advances in Robot Kinematics, 2024, Ljubljana (Slovenia), in Advances in Robot Kinematics 2024. ARK 2024, Vol 31 of Springer Proceedings in Advanced Robotics, pp. 399-406, 2024, Springer, Cham.

    Open/Close abstract Abstract Info Info pdf PDF

  • S. Moreno, L. Ros and E. Celaya. Collocation methods for second and higher order systems. Autonomous Robots, 48(2): 1-20, 2024.

    Open/Close abstract Abstract Info Info pdf PDF

  • S. Sarabandi and F. Thomas. On closed-form solutions to the 4D nearest rotation matrix problem. Mathematical Methods in the Applied Sciences, 47(3): 1248-1256, 2024.

    Open/Close abstract Abstract Info Info pdf PDF

  • F. Thomas and J.M. Porta. The inverse kinematics of lobster arms. Mechanism and Machine Theory, 196: 105630, 2024.

    Open/Close abstract Abstract Info Info pdf PDF

  • J.M. Porta and F. Thomas. Finding the common tangents to four spheres via dimensionality reduction, 19th International Symposium on Advances in Robot Kinematics, 2024, Ljubljana (Slovenia), in Advances in Robot Kinematics 2024. ARK 2024, Vol 31 of Springer Proceedings in Advanced Robotics, pp. 113-120, 2024, Springer, Cham.

    Open/Close abstract Abstract Info Info pdf PDF

  • S. Moreno. Collocation methods for the synthesis of efficient and graceful robot motions, 2024 IRI Doctoral Day, 2024, Barcelona, pp. 12.

    Open/Close abstract Abstract Info Info pdf PDF

Computational Robotics Laboratory

The COMPUTATIONAL ROBOTICS lab was created to investigate the computational and implementation aspects that arise in the design, construction, and control of complex robotic systems. Among these systems we find serial, parallel, or locomotive robots, intelligent prostheses, biomechanical support systems for movement or rehabilitation, or other robots that, due to their sensory and compliance capacities, can safely interact with humans in an agile manner. The activity of the lab focuses on the analysis and construction of robotic prototypes to validate new algorithms related, but not limited to, positional and singularity analysis, workspace determination, collision detection, forward and inverse kinematics or dynamics, singularity-robust navigation, or planning and optimal control of robot trajectories.

Computational Robotics Laboratory
Group photo

Researchers

PhD Students

Master Students

TFG Students

Support Staff